1. Flächenberechnungenmit Hilfe von Integralen
Versuche nun selbst die beiden Graphen 
und 
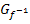in ein gemeinsames Koordinatensystem zu zeichnen! Deine Zeichnung sollte im Prinzip so aussehen, wie die folgende Abbildung.
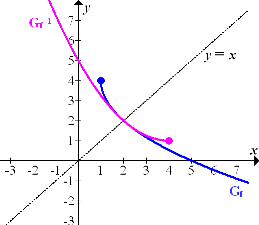
Abb.:Graph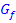 
der Funktion 
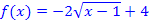und Graph 
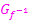der Umkehrfunktion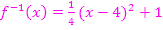 
Zu 10d.)
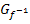In Teilaufgabe 10c.) wurden die beiden Graphen und in ein gemeinsames Koordinatensystem gezeichnet. In der folgenden Zeichnung kannst du auch das Flächenstück sehen, das im I. Quadranten von und 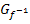mit den Koordinatenachsen eingeschlossen wird. Es ist grün markiert und setzt sich aus den Flächen 
und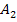 
zusammen.
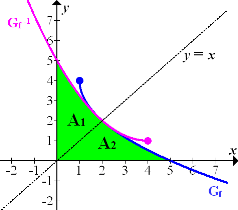
Um den Inhalt des grünen Flächenstücks berechnen zu können, müssen wir vorweg die x-Koordinate des Schnittpunkts der beiden Funktionen 
und 
ermitteln. Dieser Wert entspricht der oberen Integrationsgrenze. Normalerweise berechnet man den Schnittpunkt zweier Funktionen, indem man die Funktionen gleichsetzt. Will man den Schnittpunkt von Funktion und Umkehrfunktion ermitteln, könnte man demnach und gleichsetzen und dann nach x auflösen. Leider ergeben sich beim Gleichsetzen von und oft Gleichungen, die sich gar nicht oder nur sehr schwer nach x auflösen lassen. Daher wählen wir einen anderen Rechenweg.
Da der Graph 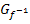durch Spiegelung von an der Winkelhalbierenden y = x entsteht, können sich und 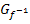zwangsläufig nur auf der Winkelhalbierenden schneiden. Eventuell vorhandene Schnittpunkte einer Funktion mit ihrer Umkehrfunktion liegen immer auf der Winkelhalbierenden y = x. Daher lassen sich gemeinsame Punkte von 
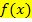und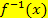 
leichter berechnen, indem man eine der beiden Funktionen 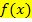oder 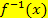mit der Winkelhalbierenden y = x gleichsetzt. An Stelle von 
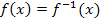kann demnach entweder die Gleichung 
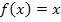oder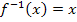 
gelöst werden. In diesem Fall entscheiden wir uns für das Gleichsetzen von 
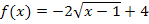mit der Winkelhalbierenden y = x. So können wir hier auch das Lösen von Wurzelgleichungen üben.
Berechnung des Schnittpunkts von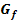 
und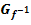 
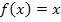
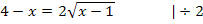
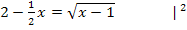
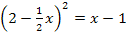
Vorsicht:Die linke Seite der Gleichung muss mit der zweiten binomischen Formelausgerechnet werden!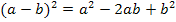 
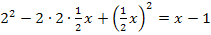
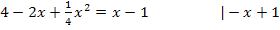
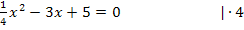
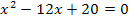
Wir verwenden die Mitternachtsformel, um die Gleichung nach x aufzulösen.
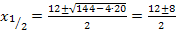
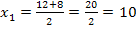
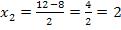
Nun muss unbedingt die Probe durchgeführt werden. Bei Wurzelgleichungen können nämlich sogenannte Scheinlösungen auftreten. Das sind Werte, die sich am Ende der Rechnung für x ergeben, die jedoch nicht Lösung der Wurzelgleichung sind, für die sich also bei der Probe ein Widerspruch ergibt. (Das liegt nicht daran, dass wir einen Fehler in unserer Rechnung haben, sondern daran, dass das Quadrieren einer Gleichung streng genommen keine Äquivalenzumformung ist.)
