1. Flächenberechnungenmit Hilfe von Integralen
Wie verändert sich der Graph weiter, wenn man nun auch noch mit der Zahl 2 multipliziert? Durch welche Abbildung ergibt sich nun aus dem Graph von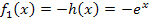 
der Graph der Funktion 
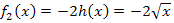? Jeder y-Wert von 
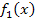wird nun verdoppelt. Das entspricht einer Streckung des Graphen von 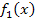entlang der y-Achse. Der Graph von 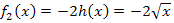liegt komplett im IV. Quadranten. Allerdings verläuft der Graph von 
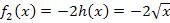durch die Punkte (1|-2) und (4|-4). Etwas weiter unten ist auch der Graph der Funktion 
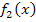dargestellt. Siehe 3. Abb.!
Durch welche Abbildung erhält man aus dem Graphen von 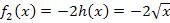den Graph der Funktion 
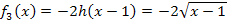? Man erhält den Graphen von 
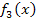, indem man den Graphen von 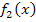um 1 nach rechts verschiebt. Das wird klar, wenn man sich überlegt, was man einerseits bei 
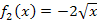und andererseits bei 
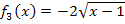einsetzen muss, um jeweils den gleichen y-Wert zu erhalten. Bei 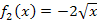muss man zum Beispiel x = 0 wählen, um den y-Wert 0 zu erhalten, währenddessen man bei 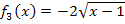die Zahl x = 1 einsetzen muss, um wieder den gleichen y-Wert 0 zu erhalten. Durch eine Verschiebung von 
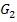um 1 nach rechts ergibt sich 
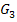. Vergleiche dazu die 4. Abb.!
Wie wirkt sich nun die Addition der Konstanten 4 aus? Addiert man zur Funktion 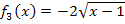die Zahl 4, erhält man die Funktion 
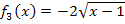. Zu jedem y-Wert von wird jeweils die Zahl 4 dazugezählt. Dadurch verschiebt sich der Graph von 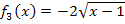um 4 nach oben. Durch eine Verschiebung von 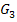um 4 nach oben ergibt sich 
. Siehe 5. Abb.!
Die Funktion kann somit als an der x-Achse gespiegelte, entlang der y-Achse gestreckte, um 1 nach rechts und um 4 nach oben verschobene Wurzelfunktion 
angesehen werden: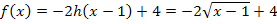 
Zusammenfassung aller Abbildungen, die von der Wurzelfunktion zur Funktion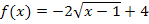 
führen:
Hier die Graphen der einzelnen Funktionen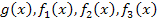 
und 
:
1. Abb.:Graph der Wurzelfunktion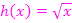 
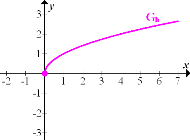
2. Abb.:Durch Spiegelung von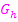 
an der x-Achse entsteht der Graph 
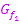der Funktion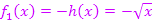 
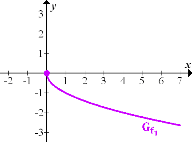
3. Abb.:Durch Streckung von 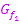entlang der y-Achse mit dem Faktor 2 ergibt sich der Graph der Funktion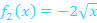 
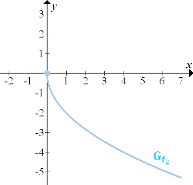
4. Abb.:Durch Verschiebung von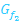 
um 1 nach rechts ergibt sich der Graph der Funktion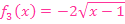 
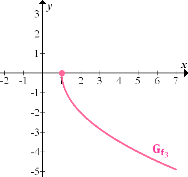
5. Abb.:Durch Verschiebung von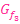 
um 4 nach oben ergibt sich der Graph der Funktion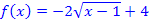 
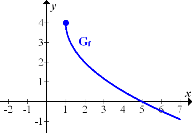
Nun haben wir den Graph in ein Koordinatensystem gezeichnet. Den Graph der Umkehrfunktion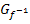 
erhältst du durch Spiegelung von an der Winkelhalbierenden des I. und III. Quadranten y = x .Am besten kannst du an der Winkelhalbierenden y = x spiegeln, indem du die Koordinaten einiger Kurvenpunkte von ermittelst und dann jeweils x- und y-Koordinate vertauschst. So erhältst du einige Punkte der Umkehrfunktion. Es wird sich dadurch der fallende Ast einer Parabel ergeben. (Vergleiche Teilaufgabe 10b.)
