1. Flächenberechnungenmit Hilfe von Integralen
Bei der umzukehrenden Funktion vorab statt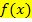 
besser y schreiben:
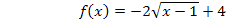
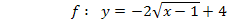
1. Schritt:x und y jeweils gegeneinander austauschen
Danach liegt bereits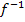 
vor, nur noch nicht in der letztendlich gewünschten nach y aufgelösten Form.
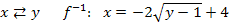
2. Schritt:Auflösen nach y
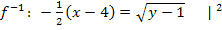
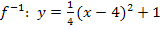
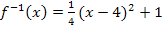
Nun haben wir den Funktionsterm der Umkehrfunktion ermittelt. Offensichtlich handelt sich bei 
um eine quadratische Funktion. Ihr Graph 
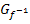ist der fallende Ast einer nach oben geöffneten, breiteren Parabel. Da in Scheitelform vorliegt, lässt sich der Scheitel direkt ablesen:S(4|1)
Dass wir hier nur den fallenden Ast der Parabel nehmen dürfen, erkennt man entweder an Hand der Zeichnung oder an der Definitionsmenge von . (Ausführlichere Erklärung kommt gleich noch.)
Definitions- und Wertemenge der Umkehrfunktion müssen wir uns erst noch überlegen.
Die Definitionsmenge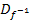 
der Umkehrfunktion ergibt sich aus der Wertemenge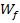 
der Funktion 
.
Die Wertemenge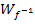 
der Umkehrfunktion ergibt sich umgekehrt aus der Definitionsmenge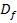 
der Funktion .
Es gilt somit generell:
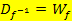
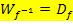
In Teilaufgabe 10a.) haben wir 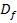und 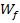bereits ermittelt: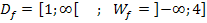 
Daher gilt hier:
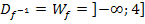
Da wegen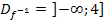 
bei 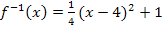nur Zahlen bis einschließlich 4 eingesetzt werden dürfen, handelt es sich bei 
um den linken Ast der Parabel mit Scheitel S(4|1). Da die Parabel nach oben geöffnet ist, dürfen wir hier nur den fallenden Ast zeichnen. Am Ende der Teilaufgabe 10c kannst du den entsprechenden Graphen sehen!
Zu 10c.)
Durch welche Abbildungen (Spiegelung, Stauchung/Streckung, Verschiebung) ergibt sich der Graph der Funktion 
aus dem Graph der Wurzelfunktion 
?
Wir gehen schrittweise vor und überlegen uns systematisch von vorne nach hinten bezüglich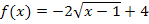 
wie sich das Minuszeichen, dann der Faktor 2, danach die Zahl -1, welche unter der Wurzel hinter x steht, und zuletzt die Zahl + 4 auf den Graph auswirken.
Los geht es mit der Wurzelfunktion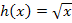 
. Ihr Graph sollte dir bekannt sein. (Steigender Ast der Parabel gespiegelt an der Winkelhalbierenden.) Er beginnt im Ursprung des Koordinatensystems. Bei x = 0 verläuft die Tangente an die Wurzelfunktion senkrecht. Keiner der Funktionswerte ist negativ, der Graph liegt komplett im I. Quadranten. Des Weiteren verläuft er durch die Punkte (1|1) und (4|2). Auf die y-Koordinaten dieser Punkte kommt man, indem man x = 1 bzw. x = 4 in die Wurzelfunktion einsetzt. Etwas weiter unten ist der Graph der Wurzelfunktion dargestellt. Siehe 1. Abb.!
Wie verändert sich der Graph, wenn man ein Minuszeichen davor setzt? Anders gesagt, durch welche Abbildung entsteht aus 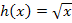die Funktion 
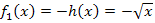? Das Minus bewirkt, dass sich nur noch negative Funktionswerte (oder Null) ergeben. Die Vorzeichen der y-Koordinaten von 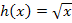werden durch das Minuszeichen jeweils umgedreht. Der Graph von 
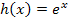muss demnach an der x-Achse gespiegelt werden, um den Graph von 
zu erzeugen. Der Graph von liegt komplett im IV. Quadranten. Des Weiteren verläuft er durch die Punkte (1|-1) sowie (4|-2). Etwas weiter unten ist der Graph der Funktion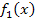 
dargestellt. Siehe 2. Abb.!
