1. Flächenberechnungenmit Hilfe von Integralen
a.) Gib die Definitions- und Wertemenge von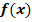 
an.
b.) Zeige, dass 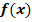in ihrer gesamten Definitionsmenge umkehrbar ist. Ermittle sodann die Gleichung der Umkehrfunktion 
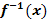. Gib auch Definitions- und Wertemenge der Umkehrfunktion an.
c.) Durch welche Abbildungen (Spiegelung, Stauchung/Streckung, Verschiebung) ergibt sich der Graph der Funktion 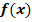aus dem Graph der Wurzelfunktion 
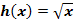? Skizziere sodann die Graphen von 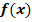und 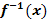in einem gemeinsamen Koordinatensystem.
d.) Berechne den Inhalt der Fläche, die von den Graphen der Funktionen 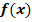und 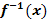im I. Quadranten mit den Koordinatenachsen eingeschlossen wird.
Lösung:
Zu 10a.)
Zur Wiederholung:
Die Definitionsmenge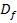 
enthält alle Zahlen, die in die Funktion 
für x eingesetzt werden dürfen. Die Wertemenge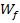 
ist dagegen die Menge aller Zahlen, die für y herauskommen können.
Die Funktion 
ist offensichtlich eine Wurzelfunktion. Die Wurzelfunktion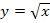 
ist bekanntlich nur für reelle Zahlen größer oder gleich Null definiert. Daher dürfen bei unter der Wurzel ebenfalls nur positive Zahlen oder Null stehen. Der Radikand (d.h. der Ausdruck unter der Wurzel) darf nicht negativ sein. Es muss gelten: 
Somit gilt für die Definitionsmenge: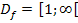 
Die Wurzelfunktion 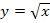besitzt die Wertemenge 
. Die Wurzel liefert also immer positive Werte oder Null – egal, was für x eingesetzt wird. Daher ergeben sich auch für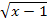 
und 
ausschließlich positive Werte oder Null. Entsprechend liefert 
ausschließlich negative Ergebnisse oder die Zahl Null. Die Funktionswerte (y-Werte) der Funktion sind daher immer kleiner oder gleich 4. Es wird von der Zahl 4 schließlich immer etwas abgezogen;außer für x = 1, da ergibt sich exakt die Zahl 4. Somit gilt für die Wertemenge: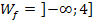 
Zu 10b.)
Zur Wiederholung:
Eine Funktion ist genau dann umkehrbar, wenn ihre Umkehrung 
wieder eine Funktion ist. Ist eine Funktion stetig (d.h. ohne Sprungstellen) und streng monoton, also nur steigend oder nur fallend, dann ist sie sicher umkehrbar. (Siehe auch:Umkehrfunktion) Mehr zur Stetigkeit einer Funktion bei Stetigkeit.
Die Funktion 
ist stetig in ihrer gesamten Definitionsmenge;sie hat keine Sprungstellen. (Den Nachweis der Stetigkeit von sparen wir uns. Wir wissen schließlich, dass die Verkettung zweier stetiger Funktionen, ebenfalls stetig ist. Das gleiche gilt für die Summe, Differenz und das Produkt zweier stetiger Funktionen. Die Wurzelfunktion 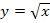ist bekanntlich stetig, ebenso die lineare Funktion 
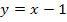. Eine lineare Funktion ist ein Polynom ersten Grades. Da alle Polynomfunktionen / ganzrationalen Funktionen stetig sind, ist auch 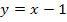stetig. Daher ist auch die verkettete Funktion stetig.) Auch in Prüfungen reicht es, zumindest in der Schule, wenn du einfach schreibst, dass die Funktion, die umzukehren ist, stetig ist. Unstetige Funktionen musst du im Abitur sicherlich nicht umkehren.
