1. Flächenberechnungenmit Hilfe von Integralen
Abb. 1b.) Die Graphen 
und 
derParabel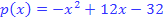 
und der Tangente 
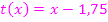mit bei x = 4 aufgeteiltem Flächenstück
Die insgesamt gesuchte Fläche setzt sich zusammen aus zwei Flächenstücken:Dem größeren lilafarbenen Flächenstück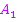 
, welches zwischen der Tangente 
, der x-Achse und der senkrechten Geraden x = 4 liegt, und dem kleineren hellblauen Flächenstück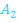 
, das auf der linken Seite von der senkrechten Geraden x = 4 begrenzt wird, auf der rechten Seite von der senkrechten Geraden x = 5,5 , oben von der Tangente und unten von der Parabel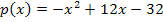 
. Es muss also erstens die Fläche zwischen der Tangente 
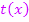und der x-Achse von der Nullstelle der Tangente x = 1,75 bis zu der Gerade x = 4 berechnet werden und zweitens die Fläche zwischen 
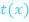und der Parabel 
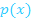, welche linksseitig von der Geraden x = 4 und rechtsseitig von der Geraden x = 5,5 (der x-Koordinate des Berührpunktes B) begrenzt ist.
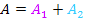
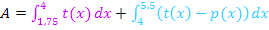
Bevor wir integrieren, fassen wir den Integranden des zweiten Integrals soweit möglich zusammen. Dazu muss natürlich erst die Klammer mit dem Minus davor aufgelöst werden, d.h. Vorzeichen innerhalb der Klammer umdrehen.
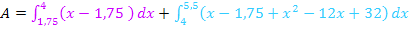
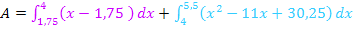
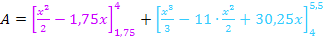
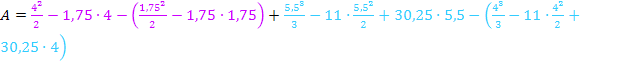
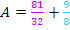
Die gesuchte Fläche hat einen Inhalt von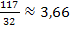 
.
Anmerkung:
Die lilafarbene Fläche 
hätte man anstatt mit dem Integral auch mit der Formel für den Flächeninhalt eines Dreiecks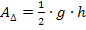 
ermitteln können.
Da es sich um ein rechtwinkliges Dreieck handelt, ist es am praktischsten, als Grundlinie g und zugehöriger Höhe h die beiden Katheten zu verwenden. Als Grundlinie sehen wir hier die waagrechte Kante des lilafarbenen Dreiecks an, welche von x = 1,75 bis x = 4 verläuft. Die zugehörige Höhe ist dann die senkrecht verlaufende Kante, die das Dreieck rechts begrenzt. Vergleiche Abb. 1b!
Die Länge der Grundlinie erhält man, indem man die beiden x-Koordinaten x = 1,75 und x = 4 voneinander abzieht: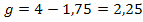 
Die Länge der Höhe ergibt sich aus dem Funktionswert der Funktion an der Stelle x = 4. Somit gilt: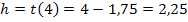 
Die beiden Katheten des lilafarbenen Dreiecks sind zufälligerweise gleich lang;das Dreieck ist gleichschenklig. Nun lässt sich der Flächeninhalt des lilafarbenen Dreiecks leicht ermitteln.
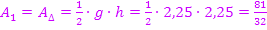
Es ergibt sich logischerweise der gleiche Wert für wie oben bei der Berechnung mit dem Integral. Zu muss natürlich noch die Fläche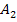 
addiert werden, um die gesamte gesuchte Fläche zu erhalten. 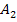kann allerdings nur mit Hilfe der Integralrechnung berechnet werden, wie oben schon vorgeführt.
Flächenberechnung nach der 2. Methode
Betrachte dazu noch einmal Abb. 1c! (Die Farbbeschreibung der einzelnen Flächen im Folgenden bezieht sich ausschließlich auf diese Abbildung.)
