1. Flächenberechnungenmit Hilfe von Integralen

Des Weiteren ist in Abb. 1c.) ein Flächenstück schwarz schraffiert. Wir nennen es im Folgenden . Dies ist eine Fläche, die zwischen Parabel und x-Achse liegt. Wir können deshalb mit Hilfe des Integrals von 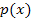berechnen. Rechtsseitig ist die Fläche durch die in der Abbildung eingezeichnete Gerade x = 5,5 begrenzt. Diese Gerade verläuft senkrecht zur x-Achse und durch den Punkt B. Die x-Koordinate des Punktes B, d.h. x = 5,5 ist die obere Grenze des Integrals. Die kleinere Nullstelle der Parabel x = 4 ist die untere Grenze. (Die Nullstelle der Parabel und die x-Koordinate des Punktes B müssen wir noch ausrechnen.)

Von der rosa schraffierten dreieckigen Fläche ziehen wir dann die schwarz schraffierte Fläche ab.

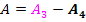
Du kannst nun selbst entscheiden, welche der beiden Methoden dir besser liegt.

Bei beiden Lösungswegen benötigen wir die Nullstelle der Tangente, die x-Koordinate des Berührpunktes B von Tangente und Parabel sowie die kleinere Nullstelle der Parabel. Wir müssen sie alle vorab rechnerisch ermitteln. (Bloßes Ablesen aus der Zeichnung führt zu Punktabzug in Prüfungen!)

Rechne nun die benötigten Werte selbst aus und vergleiche dann mit der folgenden Musterlösung!

Berechnung der Nullstelle der Tangente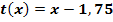

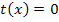
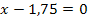
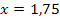
Die Tangente schneidet die x-Achse somit bei x = 1,75.

Berechnung der x-Koordinate des Berührpunktes von 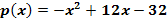und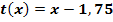

Ein Berührpunkt ist ein gemeinsamer Punkt beider Funktionen. Wir setzen die beiden Funktionsterme daher gleich.

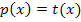
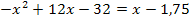
Die Gleichung enthält sowohl 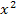als auch x und ist daher eine gemischtquadratische Gleichung. Bekanntlich lassen sich gemischtquadratische Gleichungen leicht mit der Mitternachtsformellösen. Damit wir die Mitternachtsformel anwenden können, muss die Gleichung jedoch erst nach Null umgestellt werden.

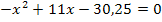
Einsetzen in die Mitternachtsformel ergibt:

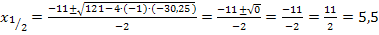
Wie zu erwarten war, da 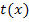schließlich eine Tangente an die Parabel 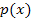ist, ergibt sich für die Diskriminante die Zahl 0 und somit genau eine (doppelte) Lösung. Der Berührpunkt B hat die x-Koordinate , wie schon in den Abbildungen 1b.) und 1c.) ersichtlich.

Berechnung der Nullstellen der Parabel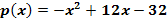

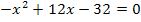
Wir verwenden wieder die Mitternachtsformel.

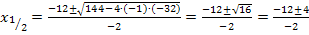
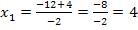
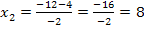
Die gesuchte kleinere Nullstelle liegt demnach tatsächlich bei x = 4 haben, so wie wir das vorher auf Grund der Zeichnung vermuteten. Die andere Nullstelle brauchen wir nicht weiter,

Nun können wir mit der Berechnung des gesuchten Flächeninhalts beginnen.

Flächenberechnung nach der 1. Methode

Betrachte dazu noch einmal Abb. 1b! (Die Farbbeschreibung der einzelnen Flächen im Folgenden bezieht sich ausschließlich auf diese Abbildung.)

---