1. Flächenberechnungenmit Hilfe von Integralen
Abb.:Der Graph 
einer Funktion 
schließt mit der x-Achse und den Geraden x = a und x = b das Flächenstück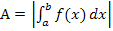 
ein. (Die Fläche liegt komplett unterhalb der x-Achse.)
Die kleinere Zahl a ist dabei die untere Grenze des Integrals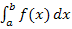 
und die größere Zahl b die obere Grenze. Das bedeutet anschaulich, dass die senkrechte Gerade 
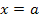die Fläche auf der linken Seite begrenzt und die zweite senkrechte Gerade 
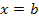die Fläche auf der rechten Seite begrenzt. Vergleiche Skizze! Wir integrieren also von links nach rechts und nehmen den Betrag des Integrals.
2. Typ: Funktion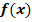 
gegeben, aber Grenzen x = a und x = b nicht angegeben
Gesucht ist die Fläche, die der Graph von 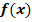mit der x-Achse einschließt. Dann muss man die Grenzen selbst berechnen.
Die Grenzen sind dann die Nullstellen von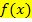 
;sie müssen vorweg berechnet, also 
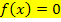gesetzt werden. Sie müssen wirklich berechnet werden! Du darfst sie nicht etwa einfach aus der Zeichnung ablesen!
Betrachten wir wieder zuerst den Fall, dass die Funktion genau zwei Nullstellen bei x = a und x = b mit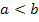 
hat. Liegt die gesuchte Fläche komplett unterhalb der x-Achse, ergibt das Integral 
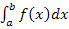nicht direkt die gesuchte Fläche, sondern erst der Betrag 
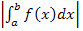. Man integriert also von der kleineren zur größeren Nullstelle und nimmt den Betrag davon. Das Integral selbst, also ohne Betrag, ergibt einen negativen Wert. Durch den Betrag wird das Ergebnis positiv, was dann dem Inhalt der Fläche zwischen und der x-Achse entspricht.
 |
 |
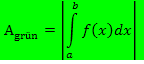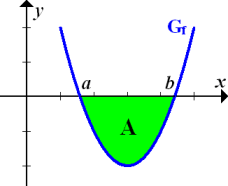
Abb.:Der Graph schließt mit der x-Achse das Flächenstück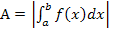 
ein. (Die Fläche liegt komplett unterhalb der x-Achse.)
Alternativer Rechenweg:
Manche Lehrer verwenden eine etwas andere Methode die Fläche zwischen und der x-Achse zu berechnen, wenn sie komplett unterhalb der x-Achse liegt:An Stelle des Betrages um das Integral schreiben sie ein Minus-Zeichen vor das Integral oder sie vertauschen die beiden Integrationsgrenzen. Auch das ist korrekt. Man kann also entweder von der kleineren Nullstelle a (untere Integrationsgrenze) zur größeren Nullstelle b (obere Grenze) integrieren und den Betrag des Integrals bilden oder man integriert umgekehrt von der größeren Nullstelle b (untere Grenze) zur kleineren Nullstelle a (obere Grenze), dann braucht man keinen Betrag.
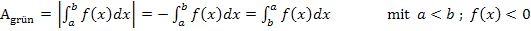
1.1.3 Fläche zwischen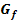 
und x-Achse im Integrationsbereich teils oberhalb und teils unterhalb der x-Achse
1. Typ: Berechnung der Fläche, welche von 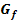, der x-Achse sowie den Geraden x = a und x = b begrenzt wird
Wenn die Funktion 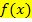zwischen x = a und x = b eine oder mehrere Nullstellen besitzt, liegt in der Regel mindestens ein Teil der gesuchten Fläche unterhalb und mindestens ein Teil oberhalb der x-Achse. Dann darf man nicht einfach 
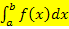berechnen, wenn man die Fläche sucht, welche von 
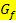, der x-Achse und den Geraden x = a und x = b begrenzt wird. Denn das Integral 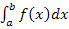würde nur die Flächenbilanz ergeben, aber nicht die gesuchte Fläche. Alle Flächenstücke, die unterhalb der x-Achse liegen, werden bekanntlich bei der Flächenbilanz negativ gewertet. (Das Integral ergibt schließlich einen negativen Wert, wenn die Fläche zwischen und der x-Achse unterhalb der x-Achse verläuft.)
