1. Flächenberechnungenmit Hilfe von Integralen
Die Summe der Flächen 
und 
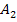ergibt die gesamte gesuchte Fläche.
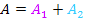
Abb. 1b.) Die Graphen 
und 
derParabel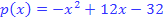 
und der Tangente 
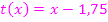mit bei x = 4 aufgeteiltem Flächenstück
Bei der lilafarbenen Fläche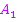 
handelt es sich um die Fläche zwischen der Funktion 
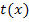und der x-Achse. Der rechte Rand von 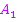ist die senkrechte Gerade x = 4. (Bei x = 4 liegt die linke Nullstelle der Parabel.) Dies ist die obere Integrationsgrenze. Die untere Grenze ist die Nullstelle der Tangente x = 1,75. Um den Inhalt der Fläche 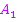zu erhalten, können wir das Integral der Funktion 
ausgehend von x = 1,75 der Nullstelle von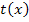 
bis zur oberen Grenze x = 4 berechnen oder einfacher mit der Formel für den Flächeninhalt eines Dreiecks 
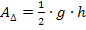arbeiten.
Bei der hellblauen Fläche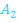 
handelt es sich um eine Fläche zwischen den beiden Funktionen 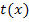und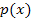 
, wobei 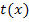die Fläche oben begrenzt. Den Inhalt der Fläche 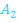bekommen wir, indem wir das Integral der oberen Funktion abzüglich der unteren Funktion, also das Integral von 
bilden. Dabei ist die senkrechte Gerade x = 4 die untere Integrationsgrenze und x = 5,5 die x-Koordinate des Berührpunktes B die obere Grenze.
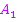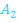Die Summe der beiden Flächenstücke und ergibt den gesuchten Flächeninhalt. Dafür müssen wir natürlich vorweg die Nullstelle der Tangente (d.h. den Wert x = 1,75), die x-Koordinate des Berührpunktes B von Tangente und Parabel (d.h. den Wert x = 5,5) sowie die kleinere Nullstelle der Parabel (d.h. den Wert x = 4) rechnerisch ermitteln.
2. Möglichkeit:
Durch den Berührpunkt B zeichnen wir eine Gerade, die parallel zur y-Achse verläuft. Beachte, dass der Berührpunkt B nicht mit dem Scheitel der Parabel zusammenfällt. Siehe dazu Abb. 1c!
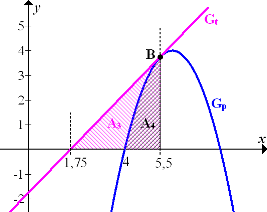
Abb. 1c.) Die Graphen und derParabel 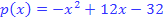und der Tangente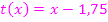
Die Fläche, die durch die beiden Graphen und die x-Achse begrenzt ist, ergibt sich aus der Differenz des rosa schraffierten Dreiecks 
und der schwarz schraffierten Fläche 
zwischen Parabel und x-Achse.
Die zusätzlich eingezeichnete senkrechte Gerade durch den Punkt B schließt zusammen mit der Tangente und der x-Achse das dreieckige Flächenstück ein (in Abb. 1c. rosa schraffiert). Den Flächeninhalt von können wir entweder mit der Formel für den Flächeninhalt eines Dreiecks 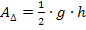ermitteln oder mittels Integralrechnung. Es handelt sich hierbei schließlich um die Fläche zwischen 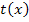und der x-Achse, ausgehend von x = 1,75 der Nullstelle von 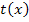bis zu x = 5,5 der x-Koordinate des Berührpunktes B. (Die Nullstelle der Tangente und die x-Koordinate des Punktes B – d.h. die Werte x = 1,75 und x = 5,5 – sind momentan nur der Zeichnung entnommen. Wir müssen sie noch ausrechnen.)
