1. Flächenberechnungenmit Hilfe von Integralen

Bisher haben wir uns nur mit Flächen zwischen einer einzigen Funktion und der x-Achse beschäftigt. Im Folgenden werden Beispiele für Aufgaben gezeigt, worin nach der Fläche zwischen zwei (oder mehr) Funktionen gefragt ist.

7. Bsp.:Fläche zwischen zwei Funktionen

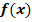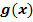Berechne den Inhalt der Fläche, den die Graphen der Funktionen und einschließen.

a.)

b.)

c.)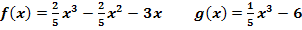

Lösung:

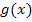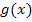Bei allen Teilaufgaben müssen vorweg die Schnittpunkte von und berechnet werden, genauer gesagt nur die x-Koordinaten (die sogenannten „Abszissen“) der Schnittpunkte. Dazu müssen jeweils und gleichgesetzt und die dadurch entstandene Gleichung nach x aufgelöst werden. So erhalten wir die Integrationsgrenzen.

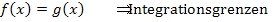
Danach müssen dann jeweils die Integrale berechnet werden. Man integriert von der kleineren zur größeren Zahl und zieht außerdem von der oberen Funktion die untere ab. Wenn man nicht weiß, welche Funktion im Bereich der Fläche oben liegt und welche unten, setzt man einfach einen Betrag um das Integral bzw. um die einzelnen Integrale.

Wenn du die Funktionen und 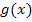gleichgesetzt hast, musst du die entstandene Gleichung 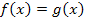vorweg oft nach Null umstellen, damit du letztendlich nach x auflösen kannst. (Ob die Null dabei auf der rechten Seite der Gleichung oder auf der linken Seite zu stehen kommt, ist logischerweise egal.)

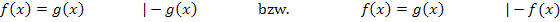
Gehen wir davon aus, dass du so umgeformt hast, dass die Null auf der rechten Seite der Gleichung steht. Dann steht auf der linken Seite der Gleichung allgemein ausgedrückt der Ausdruck 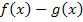, also genau das, was hinter das Integral geschrieben werden muss, falls der Graph von die Fläche oben begrenzt.

Wenn du dagegen die Gleichung 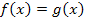so umgestellt hast, dass die Null auf der linken Seite steht, hast du auf der rechten Seite allgemein ausgedrückt den Ausdruck 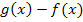stehen, also genau das, was hinter das Integral geschrieben werden muss, falls der Graph von 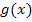die Fläche oben begrenzt.

Verwendet man den Betrag des Integrals, ist es irrelevant, welche Funktion von welcher abgezogen wird. Wenn du den Betrag verwendest, kannst du deshalb einfach denjenigen Ausdruck hinter das Integral schreiben, der bei der Schnittpunktberechnung letztendlich auf der linken Seite der Gleichung steht, natürlich vorausgesetzt, dass auf der rechten Seite der Gleichung die Zahl 0 steht. (Steht bei dir die Zahl 0 auf der linken Seite, schreibst du entsprechend denjenigen Ausdruck hinter das Integral, der bei der Gleichung rechts steht.)

Tipp:Setze die Funktionen 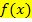und 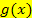gleich. Stelle die Gleichung so um, dass auf einer Seite, beispielsweise auf der rechten Seite die Zahl Null steht. Schreibe dann einfach die linke Seite der Gleichung 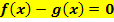bzw. 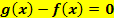hinter das Integral! Dann musst du aber Betragsstriche um das Integral setzen, um sicher zu stellen, dass das Ergebnis positiv ist und somit der Fläche zwischen 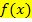und 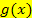entspricht.

---