1. Flächenberechnungenmit Hilfe von Integralen
Vorsicht:Es könnte nämlich auch sein, dass die Funktion zwischen a und b eine Nullstelle besitzt. Dann liegt in der Regel ein Teil der Fläche unterhalb der x-Achse und nur ein Teil oberhalb. Das Integral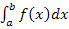 
würde in diesem Fall nicht die gesuchte Fläche, sondern nur die Flächenbilanz ergeben! Um wirklich die Fläche zu erhalten, muss das Integral an der Nullstelle geteilt werden. Bei demjenigen Flächenstück, das unterhalb der x-Achse liegt, muss der Betrag des entsprechenden Teilintegrals gebildet werden. Genaueres dazu weiter unten bei 1.1.3.
2. Typ: Funktion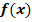 
gegeben, aber Grenzen x = a und x = b nicht angegeben
Oft findet sich die folgende Aufgabenstellung:
Gesucht ist die Fläche, die der Graph von 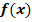mit der x-Achse einschließt.
Die Grenzen sind dann die Nullstellen von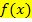 
;wir müssen sie vorweg berechnen, also 
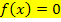setzen. Du musst die Nullstellen wirklich berechnen, also nicht einfach aus der Zeichnung entnehmen!
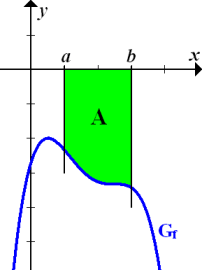
Betrachten wir zuerst den Fall, dass die Funktion genau zwei Nullstellen bei x = a und x = b mit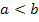 
hat. Liegt die gesuchte Fläche komplett oberhalb der x-Achse, ergibt das Integral 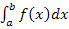direkt die gesuchte Fläche. Man integriert also von der kleineren zur größeren Nullstelle. (Die kleinere Nullstelle ist untere Integrationsgrenze, die größere Nullstelle entsprechend obere Grenze.)
 |
 |
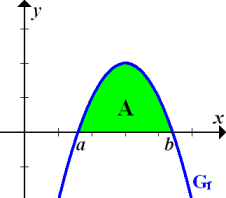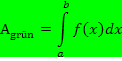Abb.:Der Graph 
schließt mit der x-Achse das Flächenstück 
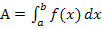ein. (Die Fläche liegt komplett oberhalb der x-Achse.)
Würde die Fläche dagegen vollständig unterhalb der x-Achse liegen, ergäbe das Integral einen negativen Wert. Man müsste dann den Betrag davon nehmen, um die Fläche zu erhalten. Das wird gleich noch genauer erklärt. Siehe:1.1.2 Fläche komplett unterhalb x-Achse
Wie man rechnen muss, wenn 
mehr als zwei Nullstellen besitzt, wird ebenfalls weiter unten erklärt. Siehe:1.1.3 Fläche teilweise oberhalb der x-Achse und teilweise unterhalb
1.1.2 Fläche zwischen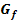 
und x-Achse im Integrationsbereich komplett unterhalb der x-Achse
Liegt die gesuchte Fläche vollständig unterhalb der x-Achse, dann entspricht das bestimmte Integral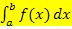 
nicht genau der gesuchten Fläche. Das Integral ist dann nämlich negativ. Da aber ein Flächeninhalt immer positiv ist, muss man den Betrag des Integrals 
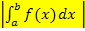bilden. Dabei gilt: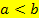 
Ob die Integrationsgrenzen schon gegeben sind oder erst vorweg berechnet werden müssen, hängt von der Aufgabenstellung ab. Es gibt beide Typen von Aufgaben.
1. Typ: Funktion 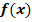und Grenzen x = a und x = b gegeben, mit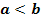 
 |
 |
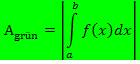