1. Flächenberechnungenmit Hilfe von Integralen
Nun stellt sich die Frage, ob wir Betragsstriche um das Integral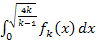 
setzen müssen oder ob wir darauf verzichten können. Warum wir nicht einfach die Betragsstriche um das Integral setzen, ohne uns Gedanken über die Notwendigkeit des Betrages zu machen, wird am Ende der Aufgabe noch erläutert. (Siehe:Wichtige Hinweise) Wir müssen uns nun überlegen, ob die gesuchte Fläche oberhalb oder unterhalb der x-Achse liegt.
Daher versuchen wir uns die Graphen der Schar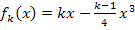 
mit k >1 vorzustellen. Es handelt sich dabei um eine Schar von Polynomen/ ganzrationalen Funktionen dritten Grades, da die höchste auftretende x-Potenz 
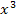ist.
Mit absteigend geordneten Potenzen lautet der Funktionsterm: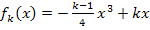 
Das Vorzeichen des Koeffizienten bei der höchsten x-Potenz, d.h. der Ausdruck vor 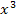, ist entscheidend über den Verlauf des Graphen. Der Ausdruck 
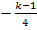ist für k >1 immer negativ, da der Zähler k – 1 für k >1 immer positiv ist und somit auch 
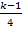positiv ist. Also muss entsprechend 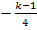grundsätzlich negativ sein.
Eine Polynomfunktion dritten Grades mit negativem Koeffizienten bei der höchsten x-Potenz, also mit negativer Zahl vor 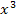, hat ungefähr den folgenden Verlauf:
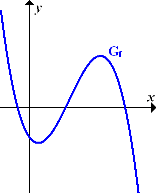
Abb.:Typischer Verlauf des Graphen 
einer Polynomfunktion dritten Grades mit negativer Zahl vor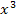
Zur Erinnerung:
Eine Polynomfunktion dritten Grades mit positivem Koeffizienten bei der höchsten x-Potenz, also mit positiver Zahl vor 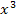, hätte dagegen ungefähr den folgenden Verlauf:
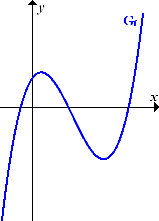
Abb.:Typischer Verlauf des Graphen einer Polynomfunktion dritten Grades mit positiver Zahl vor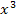
Außerdem erkennt man am Funktionsterm 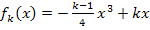, dass alle Scharfunktionen punktsymmetrisch zum Ursprung verlaufen, da nur ungerade Potenzen von x im Funktionsterm 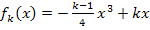auftreten. (Siehe auch:Symmetrie)
Die Graphen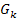 
müssen demnach ungefähr folgenden Verlauf haben:
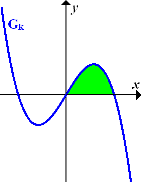
Abb.: Skizze eines der Graphen 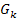der Schar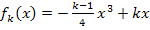
Man erkennt, dass die Fläche, die durch den Graphen 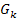und die positive x-Achse eingeschlossen ist, oberhalb der x-Achse liegt. In der Skizze ist diese Fläche grün unterlegt. (Mit „positiver x-Achse“ ist derjenige Teil der x-Achse gemeint, der rechts von der y-Achse liegt.) Wir können uns den Betrag um das Integral schenken.
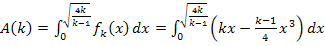
Nun müssen wir das Integral berechnen. Um eine Stammfunktion zu finden verwenden wir die Regel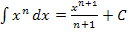 
.
Konzentriere dich beim Integrieren ausschließlich auf die Potenzen von x, denn wir integrieren nach der Variablen x. Der Scharparameter k stellt dagegen eine feste, (wenn auch momentan unbekannte) Zahl dar und keine Variable. Den Buchstaben k musst du besonders beim Integrieren wie eine konkrete Zahl behandeln. Du darfst also die Potenzen von k nicht verändern, nur die von x.
