Weitere Erklärungen zur Krümmungstabelle im 11. Bsp.

Wir haben bei der Berechnung der Wendepunkte bereits ermittelt:

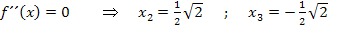
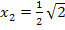Wir wollen nachweisen, dass sich das Vorzeichen von an den Stellen und 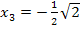ändert. Nur dann liegt jeweils eine Wendestelle vor. Deshalb fertigen wir eine Krümmungstabelle an.

Hier noch einmal die zweite Ableitung: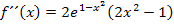

Zu Beginn sieht die Krümmungstabelle folgendermaßen aus:

x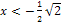
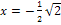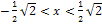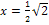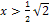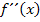		0		0

In die freien Spalten der mittleren Zeile müssen die jeweiligen Vorzeichen der zweiten Ableitung eingetragen werden. Wie kommt man aber auf die Vorzeichen von ? Am besten denkst du dir einfach eine konkrete Zahl, die in dem entsprechenden Bereich liegt, und setzt sie in ein. Je nachdem, ob sich dabei ein positives oder negatives Ergebnis ergibt, schreibst du ein Plus oder Minus in die mittlere Zeile der Krümmungstabelle unter den jeweiligen Zahlenbereich. Wenn du dir unter den Zahlen 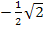und 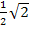nichts vorstellen kannst, gibst du sie einfach in den Taschenrechner ein und rundest sie. So ergibt sich:

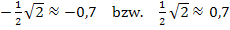
Für den Bereich 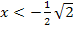kann man beispielsweise die Zahl -10 verwenden. -10 ist auf jeden Fall kleiner als 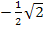. (Jede andere Zahl kleiner 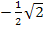hätte natürlich auch verwendet werden dürfen. Die Zahl -10 wurde ansonsten frei gewählt.) Nun setzen wir -10 in 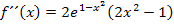ein und bestimmen das Vorzeichen.

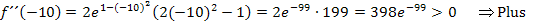
Das Plus tragen wir jetzt in die Tabelle ein.

x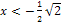
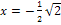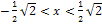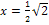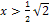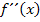		0		0

Weiter geht’s es mit dem Bereich 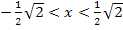. Wir wählen irgendeine Zahl aus diesem Intervall, zum Beispiel 0. Dann setzen wir diese Zahl wieder in 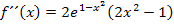ein und bestimmen das Vorzeichen.

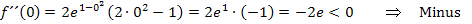
Das Minus tragen wir jetzt wieder in die Tabelle ein.

x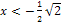
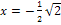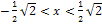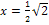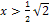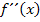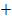		0		0

Nun noch zum letzten Intervall 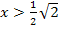. Wir wählen wieder eine Zahl aus diesem Bereich, beispielsweise 10. Die Zahl 10 ist sicher größer als  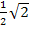. Wir setzen sie in die zweite Ableitung ein und überlegen uns das Vorzeichen.

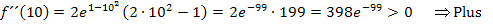
Das Plus tragen wir jetzt in die Tabelle ein.

x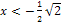
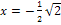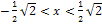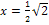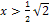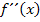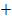		0		0

Nun haben wir alle Vorzeichen von 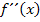bestimmt;wir müssen nur noch eintragen, wo der Graph links- bzw. rechtsgekrümmt ist.

Zur Erinnerung:

Ist die zweite Ableitung positiv 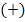, ist linksgekrümmt.

Ist die zweite Ableitung negativ 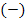, ist rechtsgekrümmt.

Da sich sowohl bei 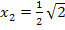als auch bei 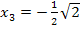das Vorzeichen von ändert, ist nachgewiesen, dass dort jeweils ein Wendepunkt (WEP) von vorliegt.

Die fertige Krümmungstabelle sieht daher folgendermaßen aus:

x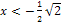
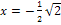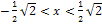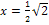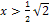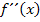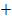		0		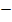0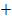
	links-gekrümmt	WEP	rechts- gekrümmt	WEP	links-gekrümmt

---