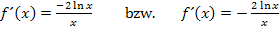Erklärungen zur Ableitung im 12. Bsp (aus GK-Abi 2005)
Wir verwenden die Kettenregel, da es sich bei der Funktion 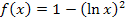 um eine verkettete (verschachtelte) Funktion handelt.
um eine verkettete (verschachtelte) Funktion handelt.
Kettenregel:Äußere Funktion ableiten, dabei die innere Funktion stehen lassen. Dann nachdifferenzieren, d.h. mit der Ableitung der inneren Funktion nachträglich multiplizieren.
Die innere Funktion ist bei der Funktion 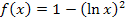 die ln-Funktion. Wie man das erkennt? Ganz einfach:Wenn du für x eine konkrete Zahl einsetzen würdest, müsstest du zuerst den Logarithmus ausrechnen, und erst danach quadrieren und von 1 subtrahieren. Das, was zuerst gerechnet werden müsste, ist die innere Funktion, also hier der ln. Wir nennen die innere Funktion
die ln-Funktion. Wie man das erkennt? Ganz einfach:Wenn du für x eine konkrete Zahl einsetzen würdest, müsstest du zuerst den Logarithmus ausrechnen, und erst danach quadrieren und von 1 subtrahieren. Das, was zuerst gerechnet werden müsste, ist die innere Funktion, also hier der ln. Wir nennen die innere Funktion 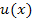 oder kurz u. Es gilt somit:
oder kurz u. Es gilt somit: 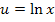
Die äußere Funktion ist dann 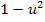 . Würde man sie nach u ableiten, ergäbe sich
. Würde man sie nach u ableiten, ergäbe sich 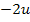 . Wir müssen aber nach x ableiten – u steht schließlich für die von x abhängige, innere Funktion
. Wir müssen aber nach x ableiten – u steht schließlich für die von x abhängige, innere Funktion 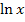 – und deshalb müssen wir noch nachdifferenzieren. D.h. wir müssen mit der Ableitung der inneren Funktion multiplizieren. Die Ableitung von
– und deshalb müssen wir noch nachdifferenzieren. D.h. wir müssen mit der Ableitung der inneren Funktion multiplizieren. Die Ableitung von 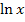 ist bekanntlich
ist bekanntlich  . Es muss daher beim Ableiten der Funktion
. Es muss daher beim Ableiten der Funktion 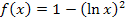 mit
mit  nachdifferenziert werden. So ergibt sich:
nachdifferenziert werden. So ergibt sich:
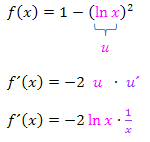
Nun kann man noch alles auf einen Bruchstrich schreiben. Ob man dabei das Minus mit dem 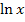 in den Zähler schreibt oder vor den Bruchstrich ist egal.
in den Zähler schreibt oder vor den Bruchstrich ist egal.