Zweite Ableitung f´´(x)
(Normalerweise ist der Funktionsgraph natürlich noch nicht bekannt, nur die Funktionsgleichung 
ist gegeben und der Graph 
ist gesucht. Man fertigt dann eine Krümmungstabelle an, um letztendlich den Graph zeichnen zu können.) Wir zäumen hier quasi das Pferd von hinten auf:Wir betrachten den Funktionsgraph in der Abbildung und überlegen uns seine Krümmung. Die Ergebnisse schreiben wir dann in die Krümmungstabelle.
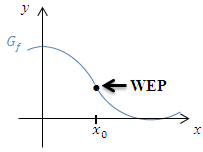
| Abbildung 1 |  |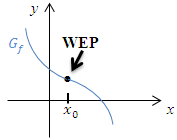
Der in Abbildung 1 dargestellte Graph verläuft links vom Wendepunkt, also im Intervall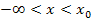 
linksgekrümmt. Das Vorzeichen der zweiten Ableitung muss in diesem Bereich somit positiv sein;wir schreiben ein Plus-Zeichen an die entsprechende Stelle in die Krümmungstabelle. Vergleiche dazu die unten gezeigte Krümmungstabelle zu Abb.1!
Am Wendepunkt, also an der Stelle 
lenkt man um;der Graph ist hier gar nicht gekrümmt. Die zweite Ableitung muss an der Stelle gleich Null sein. Deshalb schreiben wir eine Null in die mittlere Zeile direkt unter .
Rechts vom Wendepunkt, also im Bereich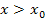 
bzw.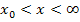 
, macht der Graph eine Rechtskurve;er ist hier rechtsgekrümmt, so dass die zweite Ableitung negativ sein muss. Wir schreiben ein Minuszeichen an die entsprechende Stelle in der Krümmungstabelle.
| Abbildung 1 | |
Krümmungstabelle zu Abbildung 1:
| x | |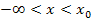
|
|
 |
 + |
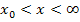0 | - |
|
linksgekrümmt | WEP | rechtsgekrümmt |
Da sich das Vorzeichen der zweiten Ableitung an der Stelle geändert hat, liegt hier definitiv ein Wendepunkt vor. Das war ja auch vom Graph her klar, da man offensichtlich an der Stelle umlenken musste, um dem Verlauf des Graphen zu folgen. Ein Wendepunt ist ja ein Punkt, wo man umlenkt.
Wenn die Funktionsgleichung gegeben ist, kommst du rechnerisch auf die entsprechenden Vorzeichen von , indem du einfach eine Zahl aus den jeweiligen Bereichen 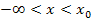bzw. 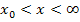in die zweite Ableitung einsetzt und dir das Vorzeichen überlegst, das dabei herauskommt. Dazu folgen weiter unten noch konkrete Beispiele.
Hier noch der zweite oben erwähnte Funktionsgraph. Er verläuft zuerst rechts- und dann linksgekrümmt. Wo der Graph rechtsgekrümmt ist, muss negativ sein. Wo der Graph linksgekrümmt ist, muss entsprechend positiv sein. Daher steht in der Krümmungstabelle zuerst ein Minus und dann ein Plus. Vergleiche dazu die Krümmungstabelle zu Abb.2!
|
Abbildung 2
|
|
Krümmungstabelle zu Abbildung 2:
| x | |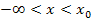
|
|
|
- |
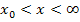0 | + |
|
rechtsgekrümmt | WEP | linksgekrümmt |
