Zweite Ableitung f´´(x)
Also niemals in eine der Ableitungen einsetzen, wenn du die y-Koordinate eines Wendepunktes von 
berechnen willst. Würdest du die vorher berechnete x-Koordinate in die erste Ableitung 
einsetzen, würdest du die Steigung der Funktion 
an der jeweiligen Stelle berechnen und nicht die y-Koordinate des Wendepunktes von . Wenn du die ermittelte x-Koordinate in die zweite Ableitung einsetzen würdest, würdest du die Krümmung an dieser Stelle erhalten, also den Wert 0. Am Wendepunkt ist die Krümmung zwangsläufig gleich Null;mit dem Ansatz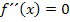 
wurde die x-Koordinate des Wendepunktes schließlich ermittelt. Also die x-Koordinaten immer jeweils in die Funktionsgleichung 
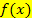selbst einsetzen, um die y-Koordinate eines Punktes von 
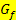zu berechnen. ist schließlich nur eine andere Schreibweise für y.
Zusätzlich muss noch nachgewiesen werden, dass wirklich ein Wendepunkt an der entsprechenden Stelle 
vorliegt. Dazu muss gezeigt werden, dass sich das Vorzeichen von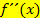 
an der Stelle 
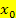tatsächlich ändert, dass sich also wirklich das Krümmungsverhalten ändert. (Ein Wendepunkt ist schließlich ein Punkt, in dem man „umlenkt“.) Das Krümmungsverhalten von stellt man am besten in einer Krümmungstabelle dar. In der Tabelle lässt sich dann leicht erkennen, ob sich das Vorzeichen von 
an der jeweiligen Stelle wirklich ändert. Nur dann liegt an dieser Stelle tatsächlich ein Wendepunkt von vor. Wenn kein Vorzeichenwechsel vorliegt, handelt es sich nur um einen sogenannten Flachpunkt FLAP von , aber eben nicht um einen Wendepunkt. (Näheres zum FLAP folgt weiter unten bei „Notwendige und hinreichende Bedingung für einen WEP“.)
Eine Krümmungstabelle wird vom Prinzip her ähnlich angefertigt wie eine Monotonietabelle, nur mit 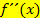an Stelle von 
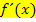. In der Krümmungstabelle werden die Krümmungsintervalle und die Vorzeichen der Krümmung von angegeben, also die Vorzeichen der zweiten Ableitung , und nicht die Vorzeichen der ersten Ableitung . Die erste Ableitung entspricht schließlich der Steigung von und nicht der Krümmung. Das Steigungs- bzw. Monotonieverhalten von wird bekanntlich in der Monotonietabelle untersucht.
Du weißt nicht mehr genau, wie man eine Monotonietabelle anfertigt? Eine Anleitung dazu findest du im 8. Bsp. des Teils:Die Ableitungsfunktion f ´(x)
Damit du sehen kannst, wie eine Krümmungstabelle aussieht, sind im Folgenden zwei Funktionsgraphen und die zugehörigen Krümmungstabellen dargestellt.
