Zweite Ableitung f´´(x)
Es können natürlich auch mehrere, verschiedene Werte für x herauskommen, also streng genommen nicht nur  sondern auch eventuell
sondern auch eventuell 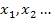 . Dann gibt es (vermutlich) mehrere Wendepunkte. Der Vorzeichenwechsel der zweiten Ableitung an der jeweiligen Stelle muss aber noch zusätzlich nachgewiesen werden, damit an der entsprechenden Stelle wirklich ein Wendepunkt von
. Dann gibt es (vermutlich) mehrere Wendepunkte. Der Vorzeichenwechsel der zweiten Ableitung an der jeweiligen Stelle muss aber noch zusätzlich nachgewiesen werden, damit an der entsprechenden Stelle wirklich ein Wendepunkt von  vorliegt.
vorliegt.
Einen Sonderfall des Wendepunktes stellt der sogenannte Terrassenpunkt dar. Der Terrassenpunkt ist ein Wendepunkt mit waagrechter Tangente. Wegen der waagrechten Tangente ist in einem Terrassenpunkt neben der Krümmung auch die Steigung gleich Null, d.h. die erste Ableitung an dieser Stelle. Bei einem Terrassenpunkt sind deshalb erste und zweite Ableitung gleich Null. Um einen Terrassenpunkt nachzuweisen, muss allerdings zusätzlich der Vorzeichenwechsel der zweiten Ableitung gezeigt werden. (Der Vorzeichenwechsel der zweiten Ableitung ist schließlich Grundvoraussetzung für die Existenz eines Wendepunktes und ein Terrassenpunkt ist ja nur ein Spezialfall des Wendepunktes.)
Wendepunkt(e) von  berechnen: berechnen:
· Damit überhaupt ein WEP vorliegen kann, muss diese Bedingung erfüllt sein. (Ob es sich wirklich um einen Wendepunkt handelt, muss noch extra nachgewiesen werden. Siehe:Nachweis des WEP) · D.h. du setzt die ermittelte(n) x-Koordinate(n) jeweils in Nachweis des WEP: · Hinreichende Bedingung für WEP: Vorzeichenwechsel von · Alternative:Der Nachweis des WEPs kann auch mit der dritten Ableitung |
Anmerkung:Ist in einer Aufgabe der Wendepunkt gesucht, müssen x- und y-Koordinate berechnet werden. Ist nur nach der Wendestelle gefragt, muss nur die x-Koordinate ermittelt werden. Sowohl bei der Frage nach dem Wendepunkt als auch nach der Wendestelle muss der Nachweis des Vorzeichenwechsels von  erbracht werden.
erbracht werden.
Um die Wendepunkte einer Funktion 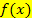 zu berechnen, setzt man daher die zweite Ableitung
zu berechnen, setzt man daher die zweite Ableitung 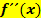 gleich Null und löst die entstandene Gleichung nach x auf. Die somit berechneten x-Koordinaten werden dann jeweils in die Funktionsgleichung
gleich Null und löst die entstandene Gleichung nach x auf. Die somit berechneten x-Koordinaten werden dann jeweils in die Funktionsgleichung  eingesetzt, um die zugehörigen y-Koordinaten zu ermitteln.
eingesetzt, um die zugehörigen y-Koordinaten zu ermitteln.

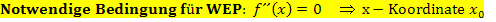
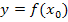
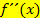
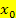
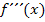 geführt werden. (Siehe:
geführt werden. (Siehe: