Zweite Ableitung f´´(x)

Die wichtigsten Zusammenhänge von und tabellarisch zusammengefasst:

x
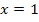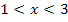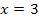Verlauf von	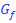links gekrümmt	WEP	rechts gekrümmt	TEP	links gekrümmt
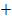		0		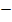0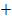
Verlauf von	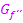oberhalb der x-Achse	Nst. mit Vzw. (x-Achse wird ge-schnitten)	unterhalb der x-Achse	Nst. mit Vzw. (x-Achse wird ge-schnitten)	oberhalb der x-Achse

Die wichtigsten Zusammenhänge von und tabellarisch zusammengefasst:

x
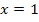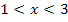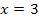Verlauf von	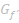str. m. steigend	HOP	str. m. fallend	TIP	str. m. steigend
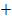		0		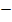0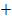
Verlauf von	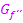oberhalb der x-Achse	Nst. mit Vzw. (x-Achse wird ge-schnitten)	unterhalb der x-Achse	Nst. mit Vzw. (x-Achse wird ge-schnitten)	oberhalb der x-Achse

Hoffentlich sind dir jetzt die Zusammenhänge des Graphen mit den Graphen und klar.

Aufgaben, in denen auch der Graph der zweiten Ableitung gezeichnet werden muss, kommen nicht so oft in Prüfungen vor. Sehr viel häufiger sind Berechnungen mit der zweiten Ableitung verlangt.

Berechnung der Wendepunkte und des Krümmungsverhaltens

Die zweite Ableitung beschreibt die Krümmung des Graphen, (also wie sich die Steigung des Graphen ändert:Zuerst steil und dann flacher steigend entspricht z.B. einer Rechtskurve). Das Vorzeichen der zweiten Ableitung gibt an, ob der Graph links- oder rechtsgekrümmt ist.

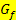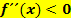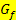ist rechtsgekrümmt, wenn
ist linksgekrümmt, wenn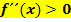

Für alle Schüler, die ein Problem haben mit der Unterscheidung von Rechts- und Linkskrümmung am Graphen:Stell dir vor, du fährst auf dem Graph von links nach rechts:Wenn du ein gedachtes Lenkrad nach rechts drehen würdest, um die Kurve zu durchfahren, ist der Graph rechtsgekrümmt. Müsstest du nach links lenken, wäre die Funktion an dieser Stelle linksgekrümmt.

An der Stelle, wo du von einer Richtung in die andere umlenkst, befindet sich ein Wendepunkt (WEP oder WP). Am Wendepunkt ist die Funktion daher weder rechts- noch linksgekrümmt:Am Wendepunkt ist die Krümmung gleich Null und das Vorzeichen von ändert sich, weil sich an dieser Stelle schließlich die Krümmung von links nach rechts oder umgekehrt ändert!

Wendepunkt: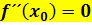

mit Vorzeichenwechsel von an der Stelle (vergleiche Krümmungstabelle!)

Terrassenpunkt (= Wendepunkt mit waagrechter Tangente):

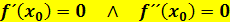
mit Vorzeichenwechsel von an der Stelle (vergleiche Krümmungstabelle!)

Hinweis:Mit ist immer eine konkrete Zahl gemeint. ist die Zahl, die sich ergibt, wenn man die Gleichung 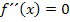nach x auflöst.

---