Zweite Ableitung f´´(x)
(Der Terrassenpunkt ist schließlich auch ein Wendepunkt;der TEP ist schließlich bloßein Sonderfall des WEP, nämlich ein WEP mit waagrechter Tangente.) Bei einem Wendepunkt gilt immer: 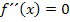 mit Vorzeichenwechsel der zweiten Ableitung. Das bedeutet, dass der Graph
mit Vorzeichenwechsel der zweiten Ableitung. Das bedeutet, dass der Graph  bei x = 1 und bei x = 3 jeweils eine Nullstelle mit Vorzeichenwechsel haben muss. Der Graph
bei x = 1 und bei x = 3 jeweils eine Nullstelle mit Vorzeichenwechsel haben muss. Der Graph  schneidet die x-Achse und berührt sie nicht nur, denn es muss an diesen Stellen schließlich ein Vorzeichenwechsel von
schneidet die x-Achse und berührt sie nicht nur, denn es muss an diesen Stellen schließlich ein Vorzeichenwechsel von  vorliegen. In den Bereichen, wo
vorliegen. In den Bereichen, wo  linksgekrümmt ist, gilt
linksgekrümmt ist, gilt 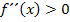 und
und  verläuft oberhalb der x-Achse. In den Bereichen, wo
verläuft oberhalb der x-Achse. In den Bereichen, wo  rechtsgekrümmt ist, gilt
rechtsgekrümmt ist, gilt 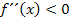 und
und  verläuft unterhalb der x-Achse. Weil
verläuft unterhalb der x-Achse. Weil  für x <1 und x >3 linksgekrümmt ist, verläuft
für x <1 und x >3 linksgekrümmt ist, verläuft  in diesen Bereichen oberhalb der x-Achse. Für 1 <x <3 ist
in diesen Bereichen oberhalb der x-Achse. Für 1 <x <3 ist  rechtsgekrümmt ist und
rechtsgekrümmt ist und  verläuft dort unterhalb der x-Achse.
verläuft dort unterhalb der x-Achse.
Stattdessen kannst du  natürlich auch als Steigung der Ableitungsfunktion
natürlich auch als Steigung der Ableitungsfunktion  auffassen. In den Bereichen, wo der Graph
auffassen. In den Bereichen, wo der Graph  der Ableitungsfunktion streng monoton fallend ist, muss
der Ableitungsfunktion streng monoton fallend ist, muss  unterhalb der x-Achse verlaufen. Weil
unterhalb der x-Achse verlaufen. Weil  nur für
nur für 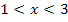 fällt, liegt
fällt, liegt  ausschließlich für
ausschließlich für 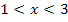 unterhalb der x-Achse. Sonst verläuft
unterhalb der x-Achse. Sonst verläuft  oberhalb der x-Achse, weil
oberhalb der x-Achse, weil  für
für 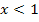 und
und 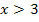 steigt. An der Stelle x = 1 und bei x = 3 hat
steigt. An der Stelle x = 1 und bei x = 3 hat  einen Hochpunkt bzw. einen Tiefpunkt;dort ist die Steigung von
einen Hochpunkt bzw. einen Tiefpunkt;dort ist die Steigung von  , also
, also  , gleich Null. Deshalb hat
, gleich Null. Deshalb hat  bei x = 1 und bei x = 3 eine Nullstelle. Weil sich das Vorzeichen der Steigung von
bei x = 1 und bei x = 3 eine Nullstelle. Weil sich das Vorzeichen der Steigung von  bei einem Extremum ändert, muss an diesen Stellen auch ein Vorzeichenwechsel von
bei einem Extremum ändert, muss an diesen Stellen auch ein Vorzeichenwechsel von  vorliegen.
vorliegen.  schneidet daher die x-Achse bei x = 1 und x = 3. Nun müsstest du auch den Graph von
schneidet daher die x-Achse bei x = 1 und x = 3. Nun müsstest du auch den Graph von  skizzieren können.
skizzieren können.
Zu deiner Kontrolle:
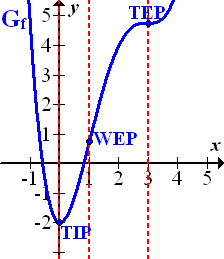
Abb.:Der Graph  der Funktion
der Funktion 
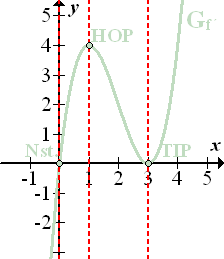
Abb.:Der Graph  der Ableitungsfunktion
der Ableitungsfunktion 
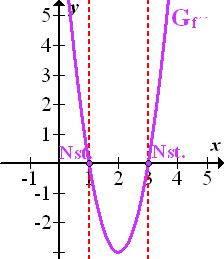
Abb.:Der Graph  der zweiten Ableitung
der zweiten Ableitung 
Falls der Tiefpunkt von  von dir nicht exakt eingezeichnet wurde, ist das nicht schlimm. Es kommt hier nur auf den groben Verlauf an. Die in den oben gezeigten Abbildungen rot gestrichelten Linien musst du selbst auch nicht unbedingt einzeichnen. Sie sollten es dir bloßerleichtern, von einem Graph auf den nächsten zu schließen. Die rot gestrichelten Linien dienten hier also nur der Verdeutlichung.
von dir nicht exakt eingezeichnet wurde, ist das nicht schlimm. Es kommt hier nur auf den groben Verlauf an. Die in den oben gezeigten Abbildungen rot gestrichelten Linien musst du selbst auch nicht unbedingt einzeichnen. Sie sollten es dir bloßerleichtern, von einem Graph auf den nächsten zu schließen. Die rot gestrichelten Linien dienten hier also nur der Verdeutlichung.
Und hier alle Graphen in einem Koordinatensystem (in der Aufgabe nicht verlangt, nur für dich, damit du sie alle auf einmal sehen kannst):
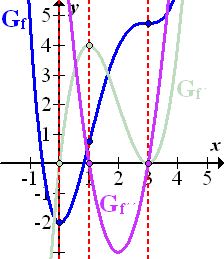
Die wichtigsten Zusammenhänge von  und
und  tabellarisch zusammengefasst:
tabellarisch zusammengefasst:
| x | 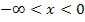 |
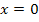 |
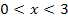 |
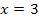 |
 |
Verlauf von 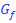 |
str. m.
fallend |
TIP | str. m. steigend | TEP | str. m. steigend |
 |
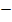 |
0 | 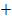 |
0 | 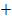 |
Verlauf von 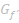 |
unterhalb
der x-Achse |
Nst.
mit Vzw. (x-Achse wird ge-schnitten) |
oberhalb der x-Achse | Nst. ohne Vzw.
(x-Achse wird nur berührt) |
oberhalb der x-Achse |

