Zweite Ableitung f´´(x)
1. Bsp.:
Gegeben ist der Graph 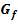 der Funktion
der Funktion 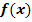 . Siehe Abbildung! Der Tiefpunkt von
. Siehe Abbildung! Der Tiefpunkt von 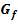 TIP(0|-2), der Terrassenpunkt TEP(3|4,75) und der Wendepunkt WEP(1|0,75) sind rot markiert. Die Wendetangente von
TIP(0|-2), der Terrassenpunkt TEP(3|4,75) und der Wendepunkt WEP(1|0,75) sind rot markiert. Die Wendetangente von 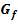 hat die Steigung 4. Zeichne zuerst den Graphen
hat die Steigung 4. Zeichne zuerst den Graphen 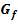 ab und zeichne dann auch die Graphen der ersten und zweiten Ableitungsfunktion in zwei weitere Koordinatensysteme!
ab und zeichne dann auch die Graphen der ersten und zweiten Ableitungsfunktion in zwei weitere Koordinatensysteme!
Hinweis:Am besten ist es, wenn du die drei Koordinatensysteme direkt untereinander zeichnest, dann kannst du nachher den Zusammenhang der Graphen von 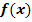 , der ersten Ableitung
, der ersten Ableitung 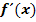 und
und 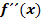 am besten erkennen.
am besten erkennen.
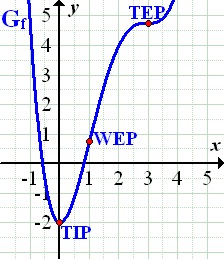
Abb.:Der Graph 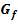 der Funktion
der Funktion 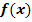
Lösung:
Nachdem du den Graphen  abgezeichnet hast, überlegst du dir, welche Punkte von
abgezeichnet hast, überlegst du dir, welche Punkte von  besonders wichtig sind für den Verlauf der beiden Ableitungsfunktionen. Das sind natürlich die bereits markierten Punkte, also der Tiefpunkt, der Terrassenpunkt und der Wendepunkt.
besonders wichtig sind für den Verlauf der beiden Ableitungsfunktionen. Das sind natürlich die bereits markierten Punkte, also der Tiefpunkt, der Terrassenpunkt und der Wendepunkt.
Wir beginnen mit den Überlegungen, die nötig sind, um auf den Graph  der ersten Ableitung zu schließen. Die erste Ableitung entspricht bekanntlich der Steigung von
der ersten Ableitung zu schließen. Die erste Ableitung entspricht bekanntlich der Steigung von  . Die Steigung von
. Die Steigung von  wird demnach als y-Koordinate von
wird demnach als y-Koordinate von  aufgefasst. An den Stellen, wo
aufgefasst. An den Stellen, wo  waagrechte Tangenten hat, ist die Steigung von
waagrechte Tangenten hat, ist die Steigung von  gleich Null und es gilt:
gleich Null und es gilt: 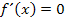 Die erste Ableitungsfunktion
Die erste Ableitungsfunktion  muss deshalb Nullstellen haben, wo
muss deshalb Nullstellen haben, wo  waagrechte Tangenten hat. D.h. weil
waagrechte Tangenten hat. D.h. weil  bei x = 0 und x = 3 waagrechte Tangenten hat, muss
bei x = 0 und x = 3 waagrechte Tangenten hat, muss  dort Nullstellen haben. In den Bereichen, wo
dort Nullstellen haben. In den Bereichen, wo  fällt, muss
fällt, muss  unterhalb der x-Achse verlaufen. Weil
unterhalb der x-Achse verlaufen. Weil  nur für x <0 fällt, liegt
nur für x <0 fällt, liegt  ausschließlich für x <0 unterhalb der x-Achse. An der Stelle x = 0 hat
ausschließlich für x <0 unterhalb der x-Achse. An der Stelle x = 0 hat  einen Tiefpunkt;dort ändert sich das Vorzeichen der Steigung von
einen Tiefpunkt;dort ändert sich das Vorzeichen der Steigung von  , also auch das Vorzeichen von
, also auch das Vorzeichen von  .
.  schneidet daher die x-Achse bei x = 0. Umgekehrt wo
schneidet daher die x-Achse bei x = 0. Umgekehrt wo  steigt, liegt
steigt, liegt  zwangsläufig oberhalb der x-Achse. Weil
zwangsläufig oberhalb der x-Achse. Weil  für
für 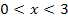 und
und  steigt, muss
steigt, muss  in diesen Bereichen oberhalb der x-Achse liegen. Im Wendepunkt W(1|0,75) steigt
in diesen Bereichen oberhalb der x-Achse liegen. Im Wendepunkt W(1|0,75) steigt  lokal am stärksten. Das bedeutet, dass die Ableitungsfunktion
lokal am stärksten. Das bedeutet, dass die Ableitungsfunktion  bei x = 1 ein Maximum haben muss. Laut Angabe hat die Wendetangente die Steigung 4. Es gilt daher:
bei x = 1 ein Maximum haben muss. Laut Angabe hat die Wendetangente die Steigung 4. Es gilt daher: 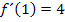
 Der Punkt (1|4) ist der Hochpunkt von
Der Punkt (1|4) ist der Hochpunkt von  . Versuche nun schon einmal den Graph
. Versuche nun schon einmal den Graph  in ein neues Koordinatensystem unterhalb von
in ein neues Koordinatensystem unterhalb von  zu skizzieren! (Die Lösung folgt etwas weiter unten!)
zu skizzieren! (Die Lösung folgt etwas weiter unten!)
Nun zum Graph  der zweiten Ableitung
der zweiten Ableitung 
![]() u kannst die zweite Ableitung entweder als Krümmung von
u kannst die zweite Ableitung entweder als Krümmung von  oder als Steigung von
oder als Steigung von  auffassen.
auffassen.
Betrachte  nun als Krümmung von
nun als Krümmung von  . Dann kannst du folgendermaßen von
. Dann kannst du folgendermaßen von  auf
auf  schließen:An der Stelle x = 1 und bei x = 3 befinden sich Wendepunkte von
schließen:An der Stelle x = 1 und bei x = 3 befinden sich Wendepunkte von  .
.

