Zweite Ableitung f´´(x)

Tipps zum Zeichnen der Wendetangente:

Beim Zeichnen der Wendetangente im Koordinatensystem ergibt sich manchmal das Problem, dass der y-Achsenabschnitt t nicht mehr in das Koordinatensystem eingezeichnet werden kann, da er betragsmäßig sehr großist und deshalb zu hoch oder tief liegt. In diesem Fall empfiehlt es sich, das Steigungsdreieck einfach vom Wendepunkt ausgehend zu zeichnen. (Durch den Wendepunkt muss die Wendetangente schließlich auf jeden Fall verlaufen.)

Hat man andererseits das Problem, dass sich zwar der y-Achsenabschnitt t gut einzeichnen lässt, jedoch die Steigung m eine absolut „krumme“ Zahl ist, so dass man kein genaues Steigungsdreieck zeichnen kann, zeichnet man einfach die Gerade durch den y-Achsenschnittpunkt und den schon markierten Wendepunkt. Dies wäre zum Beispiel hilfreich, wenn man die Wendetangente 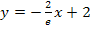aus dem 12. Bsp. in ein Koordinatensystem einzeichnen soll.

Sind sowohl m als auch t ganz „unpraktische“ Zahlen, kann man auch versuchen den Schnittpunkt der Wendetangente mit der x-Achse zu berechnen, also die Nullstelle der Wendetangente. Man setzt dazu einfach die Wendetangente gleich Null und löst dann nach x auf. Wenn sich dabei ein passabler Wert ergibt, kann die Wendetangente durch den bereits eingezeichneten Wendepunkt und die Nullstelle gezeichnet werden.

Dies waren hoffentlich genug Beispiele rund um das Thema „zweite Ableitung und ihre Anwendungen“. Bei der Kurvendiskussion werden wir die zweite Ableitung wieder brauchen.

---