Zweite Ableitung f´´(x)
Wenn dir das zu kompliziert erscheint, kannst du natürlich auch jeweils irgendeine andere Zahl aus den beiden Bereichen nehmen und das Ergebnis dann mit dem Taschenrechner ausrechnen. Gut rechnet es sich auch mit der Zahl 1, die im Intervall 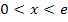 liegt.
liegt.
Das Vorzeichen des Nenners von 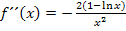 ist hier immer positiv, denn wegen der geraden Potenz kann sich dabei im Nenner nichts Negatives ergeben. (Theoretisch könnte man den Nenner somit ignorieren;er beeinflusst das Vorzeichen von
ist hier immer positiv, denn wegen der geraden Potenz kann sich dabei im Nenner nichts Negatives ergeben. (Theoretisch könnte man den Nenner somit ignorieren;er beeinflusst das Vorzeichen von  hier nicht.)
hier nicht.)
Für das Intervall 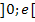 verwenden wir als Beispielzahl
verwenden wir als Beispielzahl 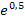 .
.
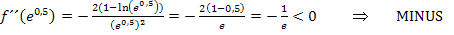
Für das Intervall 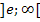 verwenden wir als Beispielzahl
verwenden wir als Beispielzahl 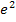 .
.
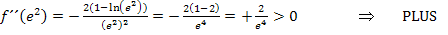
Da sich das Vorzeichen der zweiten Ableitung an der Stelle 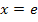 tatsächlich ändert, liegt wirklich ein Wendepunkt vor.
tatsächlich ändert, liegt wirklich ein Wendepunkt vor.
 Einziger Wendepunkt:
Einziger Wendepunkt: 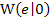
Anmerkung für Schüler, welche die dritte Ableitung 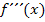 im Unterricht behandelt haben:Der Nachweis des Wendepunktes hätte auch mit Hilfe der dritten Ableitung geführt werden können. Siehe auch:Wendepunkte mit der dritten Ableitung nachweisen Allerdings dauert es ziemlich lange bei dieser Aufgabe die dritte Ableitung zu bilden, weil man dazu noch einmal die Quotientenregel anwenden müsste. Es ist in diesem konkreten Fall wohl doch eher die Untersuchung des Krümmungsverhaltens vorzuziehen.
im Unterricht behandelt haben:Der Nachweis des Wendepunktes hätte auch mit Hilfe der dritten Ableitung geführt werden können. Siehe auch:Wendepunkte mit der dritten Ableitung nachweisen Allerdings dauert es ziemlich lange bei dieser Aufgabe die dritte Ableitung zu bilden, weil man dazu noch einmal die Quotientenregel anwenden müsste. Es ist in diesem konkreten Fall wohl doch eher die Untersuchung des Krümmungsverhaltens vorzuziehen.
Berechnung der Wendetangente:
Eine Wendetangente ist wie jede andere Tangente eine Gerade und hat somit eine Gleichung der Form  .
.
Es handelt sich bei der Wendetangente bekanntlich um die Tangente an den Funktionsgraph im Wendepunkt. Ihre Gleichung wird somit genauso berechnet wie bei jeder anderen Tangente auch, nur eben im Wendepunkt. Wir ermitteln zuerst die Steigung m, indem wir die x-Koordinate des Wendepunktes in die erste Ableitung 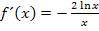 einsetzten. Danach setzt man den berechneten Wert für m, sowie die Koordinaten des Wendepunktes
einsetzten. Danach setzt man den berechneten Wert für m, sowie die Koordinaten des Wendepunktes 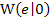 für x und y in die allgemeine Geradengleichung
für x und y in die allgemeine Geradengleichung  ein und löst nach t auf. Dadurch ergibt sich der y-Achsenabschnitt t der Wendetangente. Versuche es doch gleich mal alleine! Zu deiner Kontrolle folgt natürlich gleich der ausführliche Lösungsweg.
ein und löst nach t auf. Dadurch ergibt sich der y-Achsenabschnitt t der Wendetangente. Versuche es doch gleich mal alleine! Zu deiner Kontrolle folgt natürlich gleich der ausführliche Lösungsweg.
Berechnung der Steigung m:
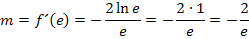
Berechnung des y-Achsenabschnitts t:

Einsetzten von 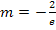 und
und 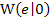 ergibt:
ergibt:
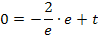
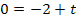
![]()
Gleichung der Wendetangente: 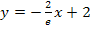
Hinweis:In der Abituraufgabe von 2005 war die Gleichung der Wendetangente sogar als Teilergebnis angegeben.
| Zusammenfassung:Wendetangente aufstellen
· Vorweg x- und y-Koordinate des Wendepunkts berechnen:
· Steigung m der Wendetangente berechnen: (Das bedeutet, dass man die x-Koordinate · y-Achsenabschnitt t der Wendetangente ermitteln:
· Gleichung der Wendetangente aufstellen: m und t in |

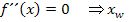 (d.h. das ergibt die x-Koordinate des WEP)
(d.h. das ergibt die x-Koordinate des WEP)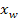 in
in  einsetzen:
einsetzen: 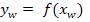
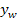 (d.h. y-Koordinate des WEP)
(d.h. y-Koordinate des WEP)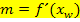
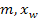 sowie
sowie 