Zweite Ableitung f´´(x)
(Das ist schließlich eine hinreichende Bedingung für die Existenz eines WEPs.) Nur wenn sich das Vorzeichen der zweiten Ableitung dort ändert, liegt wirklich ein Wendepunkt vor. (Ändert sich das Vorzeichen von 
nicht, würde es sich nur um einen Flachpunkt FLAP handeln, aber eben nicht um einen Wendepunkt WEP.)
Wir müssen daher das Krümmungsverhalten der Funktion untersuchen. Dazu fertigen wir eine Krümmungstabelle an. Beachte dabei die Definitionsmenge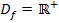 
! Das erste Intervall beginnt daher nicht bei 
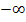sondern bei 0 (ausgeschlossen).
Hier noch einmal die zweite Ableitung: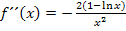 
Krümmungsverhalten von 
:
| x |  |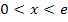
 |
 |
 |
  |
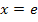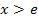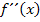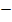0 |  |
|
rechtsgekrümmt | WEP | linksgekrümmt |
Oder in der Intervallschreibweise:
| x |  |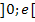
|
 |
|
|
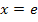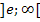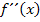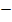0 | |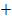
|
rechtsgekrümmt | WEP | linksgekrümmt |
Die Vorzeichen in der mittleren Zeile der Krümmungstabelle erhält man am besten, indem man sich irgendwelche konkreten Zahlen aus den beiden Bereichen 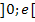und 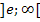überlegt und sie in die zweite Ableitung einsetzt. (Also nicht in die Funktionsgleichung 
oder in die erste Ableitung 
einsetzen, wenn du die Krümmung von untersuchen willst!)
Es bietet sich in diesem Fall an, keine natürlichen Zahlen oder Dezimalzahlen zu nehmen, sondern Zahlen der Form 
. Wir müssen hier schließlich in 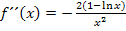einsetzen und darin kommt ein ln vor. Der ln von einer Dezimalzahl oder natürlichen Zahl lässt sich nicht gut im Kopf berechnen (abgesehen von der Zahl 1, denn es gilt ja bekanntlich:ln1 = 0) Weil sich der ln einer Zahl der Form 
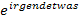im Kopf, also ohne Taschenrechner, dagegen immer sehr bequem berechnen lässt, ist es viel praktischer mit derartigen Zahlen zu arbeiten. Du weißt bestimmt: 
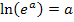Damit lässt sich z. B. 
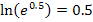leicht ausrechnen, wogegen sich z.B. 
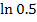nur mit einem Taschenrechner ausrechnen ließe.
Beispielsweise kann man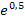 
als Zahl aus dem Intervall 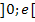verwenden, denn 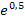ist sicher kleiner als 
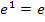, aber ganz bestimmt auch größer als 0. Als Zahl aus dem Intervall 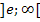könnte man zum Beispiel 
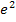wählen. Da die e-Funktion 
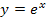streng monoton steigend ist, gilt 
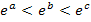für alle 
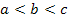und somit auch 
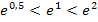, weil logischerweise für die Exponenten gilt:0,5 <1 <2 Anders formuliert:Weil der Exponent 0,5 kleiner ist als der Exponent 1, ist auch 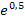kleiner als 
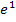. Entsprechend ist 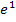wiederum kleiner als 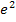weil der Exponent 1 kleiner ist der Exponent 2. Suchst du eine Zahl, die kleiner ist als 
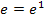, musst du nur den Exponenten kleiner machen als 1. Suchst du umgekehrt eine Zahl, die größer ist als 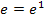, musst du bloßden Exponenten größer wählen als 1. Du kannst deshalb beispielsweise 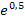als Zahl unter 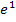verwenden und 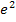als Zahl über .
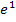