Zweite Ableitung f´´(x)
Wir leiten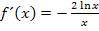 
noch einmal ab. Dazu brauchen wir die Quotientenregel. (Das Minus, das bei 
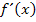vor dem Bruch steht, bleibt beim Ableiten einfach vor dem Bruchstrich stehen.)
Noch einmal zur Erinnerung die Quotientenregel in Worten:
.
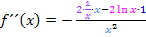
Vereinfachung von 
:
Im Zähler lässt sich beim vorderen Teil x wegkürzen.
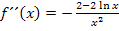
Außerdem kann im Zähler die Zahl 2 ausgeklammert werden. (Das kannst du machen, musst du aber nicht.)
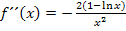
Noch einmal 
mit den ersten beiden Ableitungen auf einen Blick:
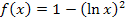
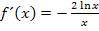
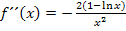
Berechnung des Extremums:
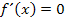(Notwendige Bedingung für ein Extremum)
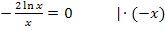
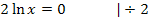
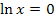
Die Umkehrfunktion zu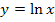 
ist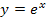 
. Funktion und Umkehrfunktion heben sich gegenseitig auf. Daher heben sich 
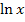und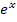 
gegenseitig auf. Die vorliegende Gleichung lässt sich deswegen nach x auflösen, indem man die e-Funktion anwendet.
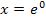
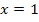
Berechnung der zugehörigen y-Koordinate:
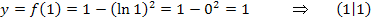
Art des Extremums ermitteln:
Wir verwenden die zweite Ableitung. (Auch die Untersuchung des Monotonieverhaltens könnte hierfür benützt werden, doch dauert das in diesem Fall länger. Die zweite Ableitung haben wir sowieso schon gebildet, da wir sie für die spätere Berechnung des Wendepunktes benötigen. Deshalb ist die Verwendung von 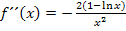hier zu bevorzugen.)
Um herauszufinden, ob an der Stelle 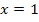ein HOP, TIP oder bloßein TEP vorliegt, setzten wir 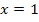in ein und bestimmen das Vorzeichen des Ergebnisses.
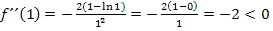
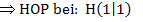
Erläuterung:Da an der Stelle 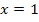die zweite Ableitung, also die Krümmung von 
, negativ ist, muss der Graph hier rechtsgekrümmt verlaufen. Es muss dort also ein Hochpunkt vorliegen. Da es sich um das einzige Extremum handelt, die Funktion stetig ist und auch keine Definitionslücke vorhanden ist, handelt es bei dem Punkt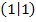 
sicherlich um einen absoluten (globalen) Hochpunkt. (Ändert eine Funktion nur an einer einzigen Stelle ihr Monotonieverhalten, hat die Funktion an dieser Stelle ein absolutes/globales Extremum. Das einzige Extremum einer stetigen Funktion ohne Definitionslücken ist somit sicher ihr absolutes Extremum.)
Absoluter HOP bei H(1|1)
Berechnung des Wendepunktes:
Hier noch einmal die zweite Ableitung: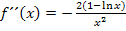
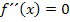(Notwendige Bedingung für WEP)
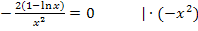
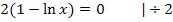
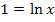
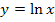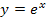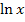Die Umkehrfunktion von ist . und 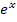heben sich gegenseitig auf. Daher lässt sich diese Gleichung nach x auflösen, indem man die e-Funktion anwendet.
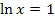
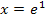
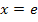
Berechnung der zugehörigen y-Koordinate:
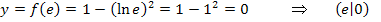
Nachweis des Wendepunktes:
Es muss gezeigt werden, dass sich an der Stelle 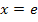das Vorzeichen der zweiten Ableitung ändert.
