Zweite Ableitung f´´(x)

(Nur wenn du eine Zeichnung machen willst, musst du die Koordinaten mit dem Taschenrechner weiter ausrechnen und dann entsprechend runden.)

Wir sprechen nun schon die ganze Zeit von den Koordinaten der „Wendepunkte“. Eigentlich ist es momentan noch gar nicht sicher, dass es sich bei den gerade ermittelten Punkten, wirklich um Wendepunkte handelt. Das müssen wir erst noch nachweisen. Damit nämlich ein Wendepunkt vorliegt, muss sich schließlich das Vorzeichen der zweiten Ableitung an den jeweiligen Stellen wirklich ändern. 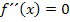ist alleine nur eine notwendige Bedingung für einen Wendepunkt, aber keine hinreichende. 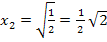Erst wenn wir einen Vorzeichenwechsel von an den Stellen und 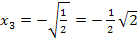jeweils nachweisen können, ist auch wirklich bewiesen, dass es sich bei 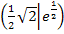und 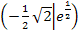Wendepunkte handelt. Läge kein Vorzeichenwechsel von vor, wäre es nur ein Flachpunkt, aber eben kein Wendepunkt. Wir müssen daher die Krümmung untersuchen. Wir stellen das Krümmungsverhalten hier, wie schon in den anderen Aufgabenbeispielen, in Form einer Krümmungstabelle dar.

Hier noch einmal die zweite Ableitung: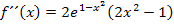

x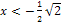
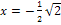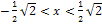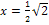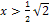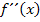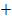		0		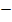0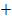
	links-gekrümmt	WEP	rechts- gekrümmt	WEP	links-gekrümmt

Es handelt sich bei den Punkten 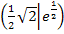und 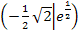tatsächlich um Wendepunkte, da sich jeweils bei 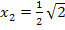und 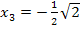das Vorzeichen von ändert.

Ergebnis: 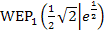und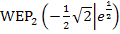

Dir ist nicht klar, wie man auf die Vorzeichen in der mittleren Zeile der Krümmungstabelle gekommen ist? Dann gehe zu:Weitere Erklärungen zur Krümmungstabelle im 11. Bsp.

Anmerkung für Schüler, die 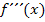im Unterricht behandelt haben:Der Nachweis des Wendepunktes hätte auch mit Hilfe der dritten Ableitung geführt werden können. Siehe auch:Wendepunkte mit der dritten Ableitung nachweisen

12. Bsp.:Nach Grundkursabitur 2005 (Bayern)

Gegeben ist die Funktion 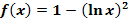. Gib die maximale Definitionsmenge 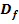an! Berechne die Art und Lage des Extremums, den Wendepunkt und die Wendetangente!

Lösung:

Zuerst überlegen wir uns die maximale Definitionsmenge der Funktion 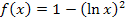. Die ln-Funktion ist nur für positive x definiert. Daher gilt auch für :

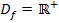
Um das Extremum und die Wendepunkte zu berechnen, brauchen wir natürlich und . Bei Extrempunkten gilt schließlich 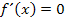und bei Wendepunkten 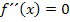Wir leiten also vorweg zweimal ab.

Berechnung von :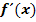

Dazu verwenden wir die Kettenregel.

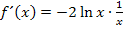
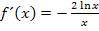
Dir ist nicht klar, wie man auf die erste Ableitung kommt?

Erklärungen zur Ableitung im 12. Bsp. (aus GK-Abi 2005)

Berechnung von :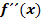

---