Zweite Ableitung f´´(x)
Das ist ja klar. Doch dazu brauchen wir die Produktregel, da es sich bei 
um ein Produkt handelt, das in beiden Faktoren die Variable x enthält.
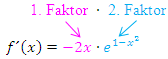
Zur Erinnerung hier noch einmal die Produktregel in Worten:
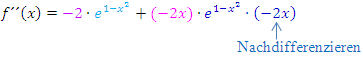
Um den zweiten Faktor (innerhalb der Produktregel) abzuleiten, wurde die Kettenregel angewendet. (Nicht vergessen:Nachdifferenzieren mit – 2 x !)
Nun vereinfachen wir die zweite Ableitung, indem wir 
ausklammern.
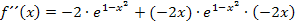
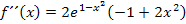
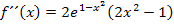
Zu schnell? Ok, dann noch einmal ganz ausführlich mit Zwischenschritten.
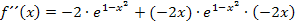
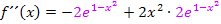
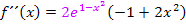
In der Klammer vertauschen wir noch die Reihenfolge der Summanden und schon haben wir 
in der oben schon gezeigten Form.
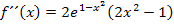
Jetzt haben wir also die ersten beiden Ableitungen gebildet und schon ´mal vereinfacht.
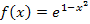
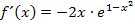
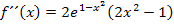
Berechnung des Extremums:
Wir setzen die erste Ableitung gleich Null.
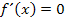
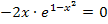
Wie löst man nun diese Gleichung? Ein Produkt ist bekanntlich gleich Null, wenn einer der Faktoren gleich Null ist. Man darf daher die Faktoren des Produkts einzeln gleich Null setzen, d.h. hier die Faktoren 
und 
. Der Faktor kann aber überhaupt nicht gleich Null werden;er ist immer positiv, egal was man für x einsetzt. (Denk daran:„e hoch egal was ist grundsätzlich positiv!“) Der andere Faktor ergibt Null, wenn man für x Null einsetzt. Daher ist die einzige Lösung:
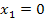
Berechnung der zugehörigen y-Koordinate:
Man setzt die x-Koordinate 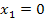in die Funktionsgleichung 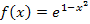ein.
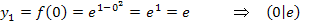
Nun wissen wir, dass 
nur bei 
einen Punkt mit waagrechter Tangente besitzt. Ob es sich dabei um einen Hochpunkt (HOP), Tiefpunkt (TIP) oder Terrassenpunkt (TEP) handelt, muss noch überprüft werden. Anders formuliert:Wir müssen die Art des Extremums ermitteln.
Überprüfung der Art des Extremums:
Man kann nun entweder eine Monotonieuntersuchung machen oder die zweite Ableitung verwenden. Da wir die zweite Ableitung bereits gebildet haben, setzten wir einfach in ein. Am Vorzeichen des Ergebnisses lässt sich dann erkennen, was für ein Punkt mit waagrechter Tangente vorliegt, also ob es sich um einen HOP, TIP oder TEP handelt.
Wir setzen die x-Koordinate 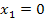in die zweite Ableitung 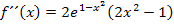ein.
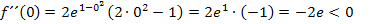
Berechnung der Wendepunkte:
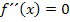
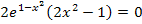
Du weißt:Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist. Man darf daher die Faktoren des Produkts, also und 
, einzeln gleich Null setzen. Der Faktor kann überhaupt nicht gleich Null werden, er ist immer positiv, egal was man für x einsetzt.
