Zweite Ableitung f´´(x)
Es muss jedoch noch überprüft werden, ob es sich bei diesen Punkten jeweils um Hoch-, Tief- oder Terrassenpunkte handelt. Dazu setzen wir die x-Koordinaten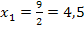 
und 
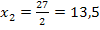jeweils in die zweite Ableitung ein.
Hier noch einmal die zweite Ableitung: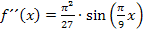 
Da Punkte streng mathematisch korrekt nur mit einem einzigen Großbuchstaben benannt werden dürfen, schreiben wir statt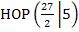 
besser 
und statt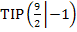 
besser 
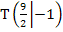. Es handelt sich um absolute (= globale) Extrempunkte, da es keine anderen Punkte des Graphen gibt, die höher als der absolute Hochpunkt bzw.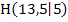 
liegen und entsprechend keine tieferen Punkte als den absoluten Tiefpunkt 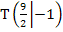bzw.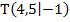 
. Das wird dir bestimmt am Verlauf des Graphen 
klar. Vergleiche dazu die folgende Abbildung!
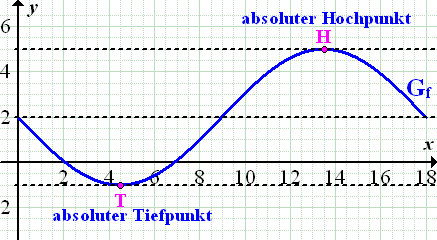
Abb.:Graph der Funktion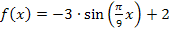 
mit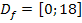 
einschließlich Hilfslinien (gestrichelt)
Anmerkung:Der Graph der Funktion 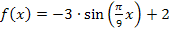lässt sich durch verschiedene Abbildungen aus dem Graph 
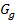der Funktion 
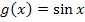herleiten. Man erhält , indem man 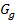an der x-Achse spiegelt, um den Faktor 9 entlang der x-Achse streckt, um den Faktor 3 entlang der y-Achse streckt und um 2 nach oben verschiebt. Mehr dazu im Kapitel Trigonometrische Funktionen:Sinus -, Kosinus – und Tangensfunktion.
Damit ist die Aufgabe gelöst. Fertig!
Nun noch ein Beispiel mit einer verketteten e-Funktion und anschließend eines mit einer verketteten ln-Funktion.
11. Bsp.:Aus Grundkurs Abitur 2003 (Bayern)
Gegeben ist die in ℝ definierte Funktion 
. Berechne Art und Lage des Extremums und die Wendepunkte der Funktion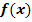 
!
Lösung:
Um das Extremum und die Wendepunkte zu berechnen, brauchen wir natürlich 
und 
. Bei Extrempunkten gilt schließlich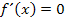 
und bei Wendepunkten 
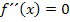Wir leiten also vorweg zweimal ab.
Berechnung von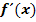 
:
Dafür verwenden wir die Kettenregel. Bei der Funktion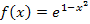 
stellt die e-Funktion die äußere Funktion dar und 
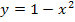die innere. Laut Kettenregel muss zuerst die äußere Funktion abgeleitet werden, wobei die innere einfach stehen bleibt. Dann muss noch nachdifferenziert werden, d.h. hier mit der Ableitung der inneren Funktion 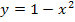multiplizieren. (Die Ableitung der inneren Funktion ist hier offensichtlich 
.) Deshalb muss noch mit multipliziert werden. So ergibt sich:
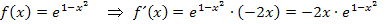
Wenn du nicht nachvollziehen kannst, wie gebildet wurde, solltest du unbedingt die Kettenregel wiederholen. Du findest nähere Erläuterungen dazu im Teil:Weitere Ableitungsregeln
Berechnung von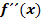 
:
Um zu bilden, muss man noch einmal ableiten.
