Zweite Ableitung f´´(x)
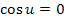
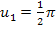
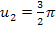
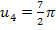
usw.
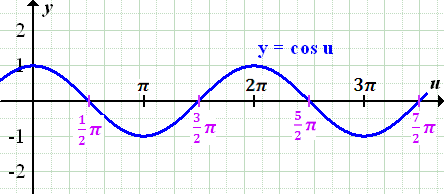
Es gibt für 
natürlich unendlich viele Lösungen, da die Kosinus-Funktion 
eine periodische Funktion ist. Sie hat die Periodenlänge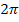 
;d.h. der Verlauf des Graphen wiederholt sich immer wieder nach 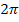. Das können wir ausnutzen, um die Lösungen kompakt zusammenzufassen. Wir nehmen nur die ersten beiden Werte 
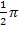und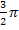 
, also diejenigen Werte, die innerhalb der ersten Periode 
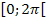liegen, und schreiben jeweils 
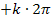dahinter. k stellt dabei eine beliebige ganze Zahl dar;sie entspricht praktisch der Anzahl der vollen Umdrehungen am Einheitskreis. (Würde man im Gradmaßund nicht im Bogenmaß rechnen, müsste man statt 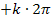entsprechend 
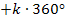schreiben. 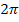entspricht bekanntlich 
.) Es gilt somit: 
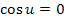
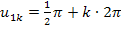
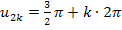
Der Zusatz 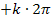drückt dabei aus, dass sich im Abstand von 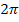immer wieder eine Nullstelle der Kosinus-Funktion befindet. Für 
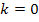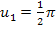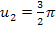ergeben sich die oben schon aufgeführten Lösungen und . Für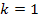 
ergeben sich die oben ebenfalls schon gezeigten Lösungen 
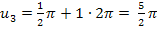und 
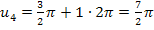. Für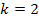 
erhält man die oben noch nicht gezeigten, weiteren Lösungen 
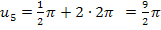und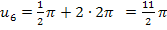 
. So könnte man nun der Reihe nach andere, ganze Zahlen für k einsetzen und man erhielte so alle Lösungen der Gleichung 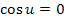. Der Zusatz 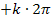stellt somit sicher, dass man wirklich alle Lösungen der Gleichung 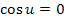mit 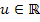beschreibt.
Wir müssen hier allerdings die Gleichung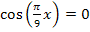 
lösen und nicht 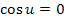. Das ist aber kein Problem. 
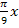entspricht einfach dem u. Daher muss gelten:
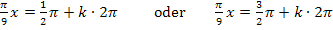
Wir müssen diese Gleichungen nun nach x auflösen. Wir dividieren daher durch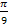 
bzw. multiplizieren mit dem Kehrwert 
. So erhalten wir:
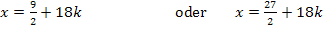
Nun gilt es die angegebene Definitionsmenge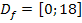 
zu beachten. Die gesuchten x-Koordinaten der Extrema müssen innerhalb dieses Intervalls liegen. Wir setzen für k einfach der Reihe nach die Zahlen 0, 1, 2 … ein und schauen, ob die jeweiligen Ergebnisse im Bereich 
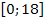liegen. Alle anderen Werte können wir vergessen.
Für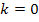
Für 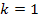und für 
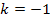würden sich Werte ergeben, die nicht mehr innerhalb der Definitionsmenge 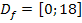liegen. Daher sparen wir uns die Arbeit.
Als nächstes berechnen wir die zugehörigen y-Koordinaten. Dazu setzen wir die soeben ermittelten x-Koordinaten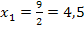 
und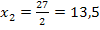 
jeweils in die Funktionsgleichung 
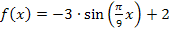ein.
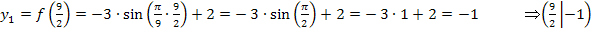
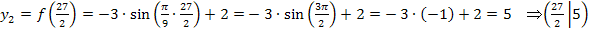
Nun kennen wir die Koordinaten aller Punkte mit waagrechten Tangenten, die in der angegebenen Definitionsmenge liegen.
