Zweite Ableitung f´´(x)
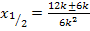
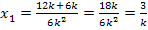
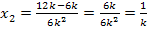
Es existieren somit zwei Punkte mit waagrechten Tangenten. Wir berechnen als nächstes die zugehörigen y-Koordinaten. Dazu müssen die x-Koordinaten jeweils in die Funktionsgleichung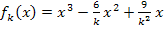 
eingesetzt werden.
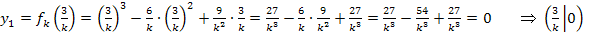
Nun muss noch untersucht werden, ob es sich bei diesen Punkten jeweils um ein relatives Extremum (HOP oder TIP) oder nur um einen Terrassenpunkt, also um kein Extremum handelt. Wir verwenden dazu die zweite Ableitung.
Art der Extrema untersuchen:
Hier noch einmal die zweite Ableitung: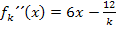 
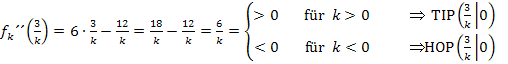
Zusammenfassung:
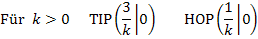
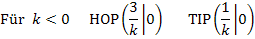
10. Bsp.:
Berechne die Koordinaten aller Extrema der Funktion. Um welche Art von Extrempunkten handelt es sich jeweils?
Lösung:
Um die Extrema der Funktion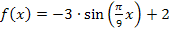 
zu berechnen, setzten wir die erste Ableitung gleich Null und lösen nach x auf. Dabei muss die Definitionsmenge 
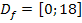beachtet werden, d.h. wir müssen alle x ermitteln, welche die Bedingung 
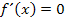erfüllen und im Intervall 
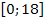liegen. Die Art der Extrema untersuchen wir mit der zweiten Ableitung. Das geht hier schneller und einfacher als mit der Monotonie. Wir benötigen daher die erste und zweite Ableitung der Funktion 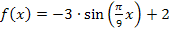. Wir ermitteln die beiden Ableitungen jeweils mit der Kettenregel. (Näheres zur Kettenregel bei Weitere Ableitungsregeln) Versuche doch gleich mal die Ableitungen selbst zu bilden! Vorsicht:Nachdifferenzieren nicht vergessen! Es handelt sich hier schließlich um eine verkettete Funktion. Der Sinus ist die äußere Funktion und 
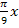die Innere.
Zur Erinnerung:Kettenregel in Worten
Äußere Funktion ableiten, dabei die Innere stehenlassen, dann mit der Ableitung der inneren Funktion nachdifferenzieren, also mit der Ableitung der inneren Funktion nachträglich multiplizieren.
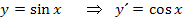
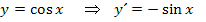
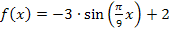
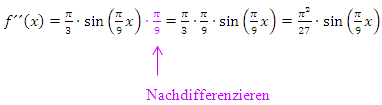
Nun kennen wir die ersten beiden Ableitungen der Funktion.
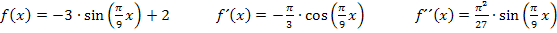
Als nächstes setzen wir die erste Ableitung gleich Null.
Notwendige Bedingung für Extrema: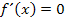
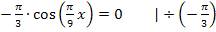
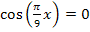
So, jetzt wird es schwierig. Wie löst man diese Gleichung nach x auf? Viele Schüler versuchen diese Gleichung mit Hilfe des Taschenrechners zu lösen. Der Taschenrechner liefert zwar mit der Tastenkombination 
das Ergebnis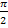 
, so dass man auf 
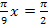kommt. Jedoch erhält man so nicht alle Lösungen der Gleichung 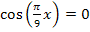. Wie bekommt man also wirklich alle Lösungen?
Am besten überlegst du dir vorab, für welche Werte von u die Gleichung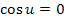 
erfüllt ist. Das kannst du zum Beispiel mit Hilfe des Graphen der Kosinus-Funktion machen. Fertige dazu eine Skizze der Kosinus-Funktion an und lies einige Nullstellen ab.
