Zweite Ableitung f´´(x)
Beim Ableiten fallen bekanntlich alle additiven Konstanten (Zahlen ohne x, die addiert oder subtrahiert werden) weg. Deshalb kann man umgekehrt beim Integrieren („Hochleiten“ oder „Aufleiten“) nicht mehr auf diese Konstanten schließen.
Das wird auch klar, wenn man versucht rechnerisch von einer gegebenen zweiten Ableitung 
rückwärts auf die zugehörige Funktion 
zu schließen.
Bsp.:
Geg.: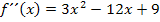 
Ges.:
Zuerst versuchen wir von der zweiten Ableitung auf die erste Ableitung zu schließen. Man muss dazu jeweils die Zahl 1 zum Exponenten dazuzählen und außerdem durch den neuen Exponenten teilen. Weil additive Konstanten beim Ableiten komplett wegfallen, können sie umgekehrt beim Integrieren nicht explizit ermittelt werden, außer es liegt noch eine weitere Information vor. Hier gibt es jedoch keine weiteren Informationen über 
. Daher müssen wir bei am Ende + C dazu schreiben.
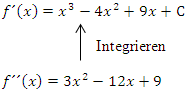
Jetzt versuchen wir soweit möglich auf die Funktion zu schließen:Wir erhöhen wieder jeden Exponenten um 1 und dividieren jeweils durch den neuen Exponenten. Weil wir wieder nicht auf die additive Konstante kommen können, schreiben wir bei am Ende + D dazu.
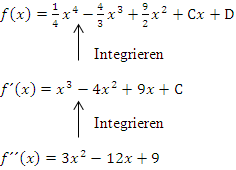
Die Zahlen C und D kann man nur dann explizit berechnen, wenn man weitere Informationen über hat. Daran müsste dir klar geworden sein, dass man von der zweiten Ableitung nicht eindeutig auf die Funktion schließen kann, solange keine weiteren Angaben über vorhanden sind.
Zusammenhang der Graphen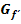 
der ersten Ableitung und 
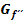der zweiten Ableitung
Die zweite Ableitung kann nicht nur als Krümmung von , sondern auch als Steigung der Ableitungsfunktion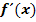 
aufgefasst werden. Die Steigung des Graphen 
der ersten Ableitungsfunktion an der jeweiligen Stelle x entspricht der y-Koordinate des entsprechenden Punktes auf dem Graphen 
der zweiten Ableitungsfunktion.
Steigung von ⇔ y-Koordinaten von
Daher ergeben sich folgende Zusammenhänge von der ersten Ableitung und der zweiten Ableitung:
| Verlauf des Graphen der Ableitungsfunktion |
Verlauf des Graphen der zweiten Ableitung |
| steigend | oberhalb der x-Achse (y-Koordinaten positiv:y = f ´´(x) >0) |
| fallend | unterhalb der x-Achse (y-Koordinaten negativ:y = f ´´(x) <0) |
| Extrempunkt
(HOP oder TIP) |
Nullstelle mit Vorzeichenwechsel, d.h. die x-Achse wird geschnitten und
nicht bloßberührt (y = f ´´(x) = 0 mit Vzw.) |
| Terrassenpunkt
(TEP) |
Nullstelle ohne Vorzeichenwechsel, d.h. die x-Achse wird berührt und
nicht geschnitten |
