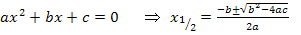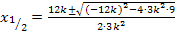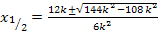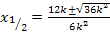Zweite Ableitung f´´(x)
Das Krümmungsverhalten ändert sich nicht. wir müssen also nur noch herausfinden, ob die Funktion immer links- oder immer rechtsgekrümmt ist. Das bedeutet, dass wir uns das Vorzeichen von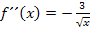 
anschauen müssen. Die Zahl 3 ist positiv;die Wurzel ergibt ebenfalls immer etwas Positives. Wegen dem Minus vor dem Bruch ist 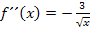für beliebige x-Werte immer negativ.
Aus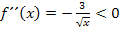 
folgt, dass die Funktion für alle x aus 
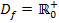rechtsgekrümmt ist.
Hinweis:Eine Krümmungstabelle war hier nicht nötig, da die Funktion ihr Krümmungsverhalten nicht ändert.
9. Bsp.:
Wir betrachten die Funktionenschar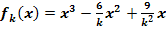 
mit 
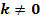. Berechne Art und Lage der relativen Extrema von 
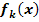in Abhängigkeit von k! (Fallunterscheidung!)
Lösung:
Wir sollen hier die relativen (= lokalen) Extrempunkte der Schar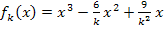 
mit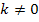 
in Abhängigkeit von k ermitteln. Das bedeutet, dass wir mit k so rechnen sollen, als wäre k eine konkrete Zahl, auch wenn wir k nicht kennen. Einsetzen darf man für k dabei allerdings nichts. Im Ergebnis kann k aber ruhig noch vorkommen. Die Problematik besteht nun darin, dass man nicht weiß, ob k für eine positive oder negative Zahl steht. Es gilt laut Angabe nämlich nur 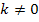. Der Scharparameter k kann daher für eine beliebige positive oder negative Zahl stehen, bloßgleich Null kann er nicht sein. (Dass k nicht gleich Null sein kann, ist sowieso klar, denn sonst würde ja der Nenner der Brüche gleich Null werden.) Gerade bei der Untersuchung der Art der Extrema muss beachtet werden, dass k sowohl negativ als auch positiv sein kann. Daher muss hierbei eine Fallunterscheidung durchgeführt werden. Also, dann mal ran an die Arbeit! Versuche es doch gleich ´mal alleine! Zur Kontrolle folgt nun der komplette Lösungsweg.
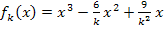
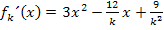
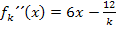
Für relative Extrema notwendige Bedingung: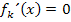 
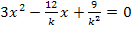
Es handelt sich bei dieser Gleichung um eine gemischtquadratische Gleichung mit der Unbekannten x, also um eine Gleichung mit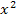 
und x (ohne Potenz). Sie lässt sich mit der Mitternachtsformellösen. Man kann die Mitternachtsformel entweder sofort anwenden oder vorher noch mit dem Hauptnenner 
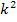multiplizieren. Wir entscheiden uns hier dafür, die Gleichung noch mit 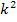zu multiplizieren, da es sich danach wesentlich leichter rechnen lässt. Durch das Multiplizieren mit 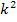fallen nämlich die Brüche weg und ohne Brüche rechnet es sich doch gleich viel besser. Die rechte Seite der Gleichung bleibt unverändert Null, denn es gilt schließlich: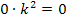 
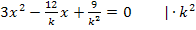
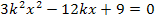
Nun setzten wir in die Mitternachtsformel ein.
Zur Erinnerung: 
