Zweite Ableitung f´´(x)
1. Möglichkeit:Erste Ableitung bilden mit der Produktregel
Zur Erinnerung:
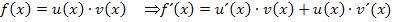
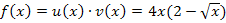
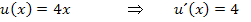
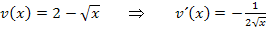Nähere Erläuterungen zur Ableitung der Wurzel
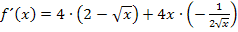
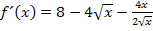
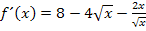
Wir machen noch den Nenner des Bruchs rational, d.h. es muss so umgeformt werden, dass keine Wurzel mehr im Nenner vorkommt. Wir Erweitern daher den Bruch mit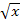 
. Dadurch fällt die Wurzel im Nenner des Bruchs weg, so dass man 
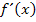nachher weiter zusammenfassen kann. Der Nenner muss hier unbedingt rational gemacht werden, also so umgeformt werden, dass keine Wurzel mehr im Nenner vorkommt. Anders könnte man 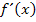nämlich nicht weiter vereinfachen.
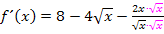
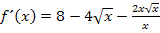
Jetzt lässt sich x kürzen. Dadurch ergibt sich:
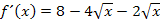
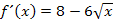
2. Möglichkeit:Erste Ableitung bilden ohne Produktregel nach geeigneter Umformung von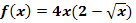 
Wir multiplizieren erst einmal aus und schreiben die Wurzel als Potenz.
Zur Erinnerung:Wegen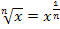 
gilt: 
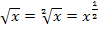
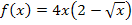
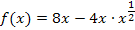
Nun wenden wir das Potenzgesetz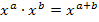 
an.
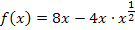
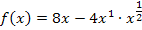
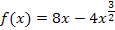
In dieser Form lässt sich die Funktion leicht mit der Regel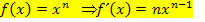 
ableiten. So ergibt sich für die erste Ableitung:
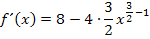
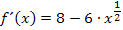
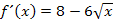
Das ist natürlich das gleiche Ergebnis, das wir auch schon oben erhalten haben. Jetzt bilden wir noch die zweite Ableitung.
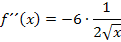
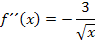
Noch einmal alles übersichtlich zusammengefasst, was wir momentan wissen:
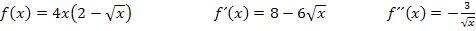
Berechnung der Extrema
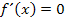
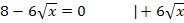
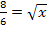
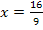
Berechnung der zugehörigen y-Koordinate:
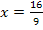Einsetzten von in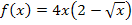
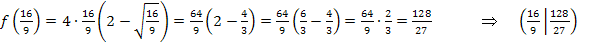
Untersuchung der Art des Extremums:
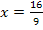Einsetzen von in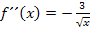 
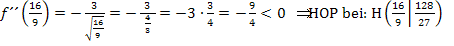
Untersuchung des Krümmungsverhaltens
Normalerweise beginnt man die Untersuchung des Krümmungsverhaltens, indem man die zweite Ableitung gleich Null setzt, um eventuell vorhandene Wendepunkte zu ermitteln. Nur in einem Wendepunkt oder bei einer Definitionslücke kann sich das Krümmungsverhalten ändern. Eine Definitionslücke liegt hier nicht vor, somit könnte sich das Krümmungsverhalten nur noch in einem Wendepunkt ändern.
Wendepunkte findet man bekanntlich durch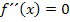 
. In diesem Fall kann die zweite Ableitung 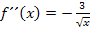aber gar nicht gleich Null werden. Ein Bruch ist schließlich gleich Null, wenn der Zähler Null ergibt. Der Zähler besteht hier jedoch nur aus der Zahl 3, enthält also gar kein x. Daher kann der Zähler nicht gleich Null werden und somit auch der ganze Bruch nicht. Es gilt für alle x aus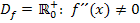 
Es existieren deshalb keine Wendepunkte.
