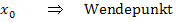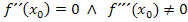Zweite Ableitung f´´(x)

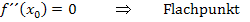
Mit Vorzeichenwechsel von an der Stelle Ohne Vorzeichenwechsel von an der Stelle

Damit du dir das besser vorstellen kannst, hier ein konkretes Beispiel eines Graphen mit einem Flachpunkt, der aber kein Wendepunkt ist.

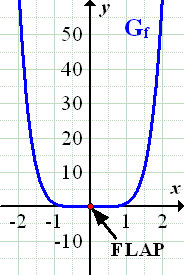
Abb.:Graph der Funktion 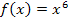mit Flachpunkt (0|0)

Achtung:Dieser FLAP ist kein WEP!

Die Funktion 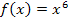hat an der Stelle 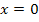zwar die Krümmung Null, aber die Krümmung ändert ihr Vorzeichen nicht. (Man lenkt nicht um.) Es liegt daher kein Wendepunkt vor, sondern nur ein Flachpunkt.

Will man bei einer gegebenen Funktion den bzw. die Wendepunkt(e) berechnen, muss man mit dem Ansatz 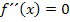beginnen, da , also die Krümmung von gleich Null sein muss, damit überhaupt ein Wendepunkt vorliegen kann. Bei einem Wendepunkt notwendig, dass 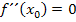gilt. Man nennt 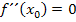die notwendige Bedingung für einen Wendepunkt.

Für einen Wendepunkt notwendige Bedingung: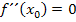

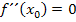Das heißt, dass diese Bedingung erfüllt sein muss, damit überhaupt ein Wendepunkt vorliegen kann. Der Graph muss an der Stelle also die Krümmung haben, damit es sich um einen Wendepunkt handeln kann. Da der Graph aber bei allen Flachpunkten keine Krümmung besitzt, ist die Bedingung 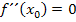auch dann erfüllt, wenn es sich nur um einen Flachpunkt, aber nicht um einen Wendepunkt handelt. Es kann sich daher an der Stelle auch nur um einen reinen Flachpunkt handeln. Von der Bedingung 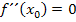kann also noch nicht sicher auf die Existenz eines Wendepunkts an der Stelle geschlossen werden. (Dazu braucht man noch eine hinreichende Bedingung.) Damit aber überhaupt ein Wendepunkt vorliegen kann, ist es zumindest notwendig, dass 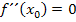erfüllt ist. Daher die Bezeichnung „notwendige“ Bedingung.

Für einen Wendepunkt hinreichende Bedingung: 1. Möglichkeit:Vorzeichenwechsel von 2. Möglichkeit:

Das heißt, dass eine dieser beiden Bedingungen ausreicht (hinreichend ist), damit man ganz sicher sagen kann, dass an der Stelle 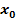ein Wendepunkt sein muss. Durch die hinreichende Bedingung ist sichergestellt, dass es sich hundertprozentig um einen Wendepunkt handelt.

Nun noch einige weitere Beispiele zu den verschiedenen Anwendungen der zweiten Ableitung.

8. Bsp.:

Berechne Art und Lage des Extremums von 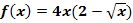mit 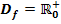. Untersuche außerdem das Krümmungsverhalten!

Lösung:

Vorweg bilden wir die erste und zweite Ableitung der Funktion. Die erste Ableitung kann entweder ohne weitere Umformung von mit der Produktregel berechnet werden oder man formt die Funktion erst einmal so um, dass man die Produktregel gar nicht benötigt. Du kannst selbst entscheiden, was dir persönlich leichter fällt. Es werden im Folgenden beide Methoden vorgeführt.

---