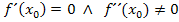Zweite Ableitung f´´(x)
Nur zusammen mit der für ein Extremum „notwendigen“ Bedingung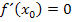 
(waagrechte Tangente) lässt die Bedingung 
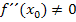eindeutig den Schluss zu, dass die Funktion 
an der Stelle 
sicher einen Extrempunkt aufweist.
Für ein Extremum notwendige Bedingung:  |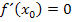
Das heißt, dass diese Bedingung erfüllt sein muss, damit überhaupt ein Extremum vorliegen kann. Ein Punkt muss eine waagrechte Tangente, also die Steigung 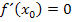haben, damit es sich um ein Extremum handeln kann. Da aber auch Terrassenpunkte eine waagrechte Tangente besitzen, erfüllen auch sie die Bedingung 
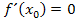. Es kann sich daher an der Stelle entweder um ein Extremum oder einen Terrassenpunkt handeln. Von der Bedingung 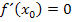kann also noch nicht sicher auf die Existenz eines Extremums an der Stelle geschlossen werden. (Dazu braucht man noch eine hinreichende Bedingung.) Damit aber überhaupt ein Extremum vorliegen kann, ist es notwendig, dass 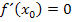erfüllt ist. Daher die Bezeichnung „notwendige“ Bedingung.
| Für ein Extremum hinreichende Bedingung:
1. Möglichkeit: Vorzeichenwechsel von
2. Möglichkeit: |
Das heißt, dass eine dieser Bedingungen ausreicht (hinreichend ist), damit man ganz sicher sagen kann, dass an der Stelle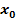 
ein Extremum sein muss.
Notwendige und hinreichende Bedingung für einen Wendepunkt
Damit an der Stelle sicher ein Wendepunkt (WEP) vorliegt und nicht etwa nur ein Flachpunkt (näheres zum FLAP siehe unten), muss neben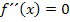 
auch ein Vorzeichenwechsel von 
an der Stelle vorliegen oder es muss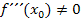 
gelten. Der Vorzeichenwechsel von ist eine sogenannte „hinreichende“ Bedingung für einen Wendepunkt. Damit meint ein Mathematiker, dass der Vorzeichenwechsel von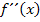 
oder die Bedingung 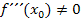ausreichend (hinreichend) sind, damit ganz sicher bei ein Wendepunkt vorliegt. Wenn nur die Bedingung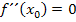 
erfüllt ist, muss jedoch nicht zwangsläufig ein Wendepunkt vorliegen. 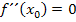bedeutet alleine nur, dass der Funktionsgraph an der Stelle die Krümmung 0 hat. Nur weil der Graph weder nach links noch nach rechts gekrümmt ist, muss hier aber noch lange kein Wendepunkt sein, es könnte sich auch nur um einen Flachpunkt (FLAP) handeln.
Ein Flachpunkt (FLAP) ist ein Punkt, wo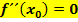 
gilt.
Bei einem Flachpunkt FLAP kann ein Vorzeichenwechsel von vorliegen, muss aber nicht. Bei einem Wendepunkt muss dagegen sein Vorzeichen ändern.
Somit ist ein Wendepunkt ein Sonderfall des Flachpunktes. Ein Flachpunkt (FLAP) mit Vorzeichenwechsel von wird eben als Wendepunkt (WEP) bezeichnet.
