Zweite Ableitung f´´(x)
Man kann die Art des Extremums in dieser Aufgabe offensichtlich wesentlich schneller mit der zweiten Ableitung ermitteln. Allerdings war es vorher ziemlich viel Arbeit die zweite Ableitung überhaupt zu bilden. Nur weil man die zweite Ableitung sowieso für die nächste Teilaufgabe zur Berechnung des Wendepunkts und für das Krümmungsverhalten braucht, ist hier die Methode mit 
zur Untersuchung der Art der Extrema zu bevorzugen.
Zu 7b.)
Berechnung des Wendepunkts:
Hier noch einmal die zweite Ableitung: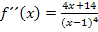 
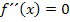
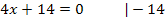
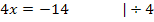
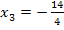
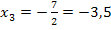
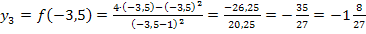
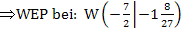
Nachweis des Wendepunkts mit Hilfe des Krümmungsverhaltens:
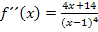
Krümmungstabelle:
Wir nehmen neben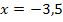 
, der x-Koordinate des (vermutlichen) Wendepunkts, auch die Definitionslücke 
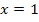in die Krümmungstabelle auf. Dann ermittelt man die Vorzeichen der zweiten Ableitung, zum Beispiel indem man aus den einzelnen Bereichen jeweils eine konkrete Zahl wählt und in 
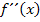einsetzt.
| x |  |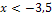
 |
 |
 |
 |
|
 |
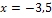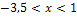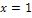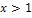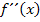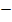0 |  + |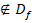
 |
 |
 |
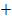rechts-gekrümmt | WEP | links-gekrümmt | POL | links-gekrümmt |
Bei 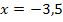liegt wirklich eine Wendestelle vor, da sich hier das Vorzeichen der zweiten Ableitung ändert. Der Punkt 
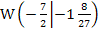ist daher der Wendepunkt der Funktion.
Notwendige und hinreichende Bedingung
Im Zusammenhang mit Extrempunkten oder Wendepunkten sprechen manche Lehrer immer wieder von einer sogenannten „notwendigen“ und einer „hinreichenden“ Bedingung. Wahrscheinlich denkst du dir dabei:Was ist denn damit bloßwieder gemeint? Im Folgenden werden die beiden Begriffe „notwendige“ und „hinreichende“ Bedingung zuerst für die Existenz eines Extremums und danach für einen Wendepunkt erklärt.
Notwendige und hinreichende Bedingung für ein Extremum
Damit an der Stelle 
sicher ein relatives Extremum (HOP oder TIP) vorliegt und nicht etwa ein Terrassenpunkt, muss zusätzlich zu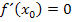 
auch entweder 
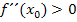(TIP) oder 
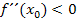(HOP) gelten. Man kann also sagen, dass bei einem Extremum 
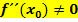gelten muss. Dies ist zusammen mit der Bedingung 
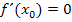eine sogenannte „hinreichende“ Bedingung für einen Extrempunkt. Damit meint ein Mathematiker, dass die Bedingungen 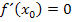und zugleich 
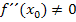ausreichend (hinreichend) sind, damit ganz sicher bei ein Extremum vorliegt. Wenn die Bedingung 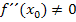alleine gilt, muss jedoch nicht zwangsläufig ein Extremum vorliegen. 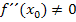bedeutet alleine nur, dass der Funktionsgraph an der Stelle nicht die Krümmung 0 hat, d.h. er muss entweder links- oder rechtsgekrümmt sein. Nur weil der Graph nach links oder nach rechts gekrümmt ist, muss hier aber noch lange kein Extremum sein. Umgekehrt muss aber der Graph nach rechts gekrümmt sein, wenn ein HOP vorliegt, bzw. er muss nach links gekrümmt sein, wenn ein TIP vorliegt.
