Zweite Ableitung f´´(x)

wir wenden noch einmal die Quotientenregel an. Um den Nenner abzuleiten, muss wieder die Kettenregel benützt werden. Das Nachdifferenzieren mit 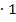spielt dabei wieder keine Rolle.

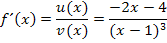
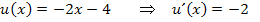
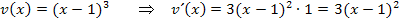
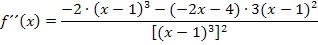
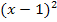Wir multiplizieren im Zähler, wie schon bei der Berechnung von , nicht sofort aus, sondern klammern den Faktor aus. Der Nenner wird mit Hilfe des Potenzgesetzes 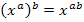vereinfacht.

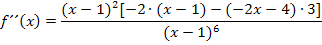
Nun kann man den Faktor 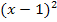kürzen, da nun im Zähler ein Produkt vorliegt.

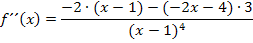
Jetzt multiplizieren wir im Zähler aus und fassen soweit möglich zusammen.

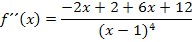
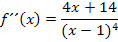
Jetzt wissen wir:

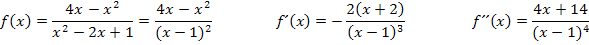
Zu 7a.)

Berechnung der Extrema:

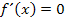
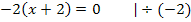
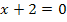
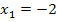
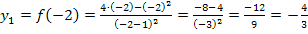
Art der Extrema untersuchen:

1. Möglichkeit:Mit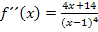

Wir setzen die soeben ermittelte x-Koordinate 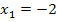in die zweite Ableitung ein und können dann am Vorzeichen des Ergebnisses erkennen, ob ein relativer (lokaler) HOP bzw. TIP oder ein Terrassenpunkt, also überhaupt kein Extremum, vorliegt.

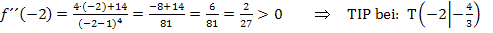
2. Möglichkeit:Mit Monotonietabelle

Hier noch einmal die erste Ableitung: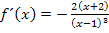

Vorsicht:Die Definitionslücke 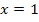muss auch in der Monotonietabelle vorkommen, nicht nur die Stelle 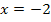, wo eine waagrechte Tangente besitzt!

Auf die Vorzeichen in der mittleren Zeile der Monotonietabelle kommst du, indem du dir jeweils eine konkrete Zahl aus den einzelnen Bereichen denkst und sie in die erste Ableitung einsetzt. Kommt dabei etwas Positives heraus, schreibst du ein Plus in die Tabelle;der Graph steigt streng monoton in dem entsprechenden Intervall. Kommt dagegen etwas Negatives heraus, schreibst du ein Minus in die Tabelle;der Graph ist in diesem Bereich streng monoton fallend.

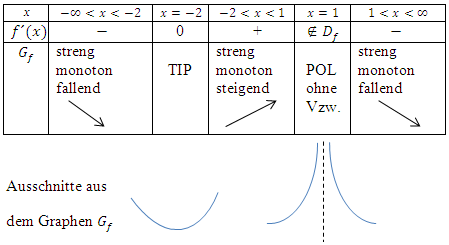
Man erkennt an der Monotonietabelle sofort, dass bei 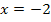ein relativer Tiefpunkt (TIP) vorliegt, da der Graph zuerst fällt und dann wieder steigt. Vergleiche dazu die Pfeile in der Monotonietabelle, die das Steigen und Fallen des Graphen symbolisieren sollen.

Bei 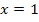ändert sich zwar das Vorzeichen der ersten Ableitung ebenfalls, jedoch liegt 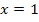nicht innerhalb der Definitionsmenge. Daher kann bei 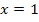kein Extremum sein;hier ist nämlich die Polstelle.

Das einzige relative Extremum von ist der Tiefpunkt .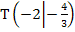

---