Zweite Ableitung f´´(x)
(Es handelt sich dabei um einen Pol ohne Vorzeichenwechsel. Weil sich die Definitionslücke nicht wegkürzen lässt, liegt ein Pol vor. Das erkennt man eigentlich erst, wenn man auch den Zähler faktorisiert, d.h. an der Form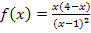 
. Da es sich um einen Pol gerader (zweiter) Ordnung handelt, liegt ein Pol ohne Vorzeichenwechsel vor. Das ist wichtig für die Monotonie der Funktion. Bei einem Pol ohne Vorzeichenwechsel ändert sich nämlich immer das Steigungsverhalten, bei einem Pol mit Vorzeichenwechsel dagegen nicht. Ein Pol ohne Vorzeichenwechsel muss daher in die Monotonietabelle mitaufgenommen werden. Die Monotonieuntersuchung kannst du anwenden, um die Art der Extrema zu untersuchen. Du kannst das jedoch auch mit der zweiten Ableitung überprüfen. Es ist hier zwar ziemlich viel Arbeit 
zu berechnen, doch wir kommen in 7b.) sowieso nicht darum herum. Da in der Teilaufgabe 7b.) auch nach dem Krümmungsverhalten und den Wendepunkten gefragt ist, müssen wir die zweite Ableitung dann sowieso berechnen, da man Wendepunkte bekanntlich mit 
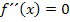ermittelt. Also können wir die zweite Ableitung auch schon in 7a.) berechnen und damit die Art der Extrema untersuchen.
Nun bilden wir vorweg die erste und zweite Ableitung. Dafür brauchen wir die Quotientenregel:
Zur Erinnerung:
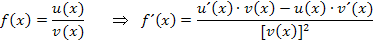
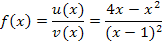
Um den Nenner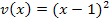 
abzuleiten, braucht man eigentlich die Kettenregel, d.h. man muss mit der Ableitung der inneren Funktion 
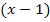nachdifferenzieren. Da die Ableitung der inneren Funktion 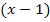jedoch 1 ist, spielt das hier keine Rolle. („Mal 1“ kann man ja weglassen.) Wenn du mit der Kettenregel Schwierigkeiten hast, kannst du den Nenner natürlich auch in der Form 
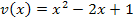ohne Kettenregel ableiten. Dann musst du nachher aus 
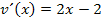allerdings die Zahl 2 ausklammern, sonst kannst du nachher nicht erkennen, dass sich im Zähler von 
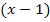der Ausdruck komplett ausklammern lässt.
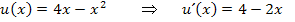
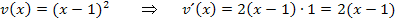
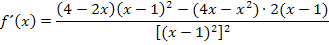
Jetzt multiplizieren im Zähler nicht aus, sondern klammern stattdessen den Ausdruck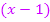 
komplett aus. Der Nenner wird mit Hilfe des Potenzgesetzes 
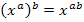vereinfacht.
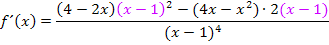
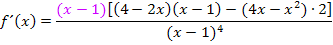
Nun kann man den Faktor 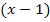kürzen, da nun im Zähler ein Produkt vorliegt.
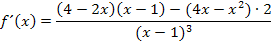
Jetzt multiplizieren wir im Zähler aus und fassen soweit möglich zusammen.
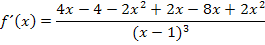
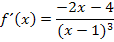
Man könnte noch die Zahl -2 im Zähler ausklammern;das muss man aber nicht unbedingt machen. Das Minus lässt sich dann vor den Bruchstrich schreiben.
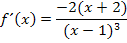
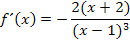
Um die zweite Ableitung zu bilden, gehen wir jedoch am besten von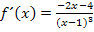 
aus.
