Zweite Ableitung f´´(x)
Damit bei  sicher ein TEP vorliegt, muss neben
sicher ein TEP vorliegt, muss neben 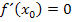 und
und 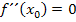 auch
auch 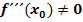 gelten.)
gelten.)
Zusammenfassung: Art der Extrema mit 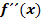 untersuchen
untersuchen
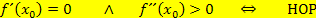

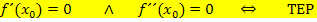 *
*
*Wenn ein Vorzeichenwechsel von  an der Stelle
an der Stelle  vorliegt bzw.
vorliegt bzw. 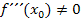 gilt.
gilt.
Mit  ist übrigens eine konkrete x-Koordinate, also eine bestimmte Zahl, gemeint. Das Zeichen
ist übrigens eine konkrete x-Koordinate, also eine bestimmte Zahl, gemeint. Das Zeichen 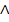 bedeutet „und zugleich“.
bedeutet „und zugleich“.
Schauen wir uns doch gleich mal ein Beispiel dazu an.
6. Bsp.:
Ermittle Art und Lage der relativen Extrempunkte der Funktion 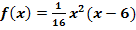 ohne Monotonieuntersuchung!
ohne Monotonieuntersuchung!
Lösung:
Bei einem Extremum verläuft die Tangente an den Funktionsgraph waagrecht, daher gilt:
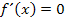
Wir müssen daher die erste Ableitung gleich Null setzen, um die x-Koordinaten der Punkte mit waagrechten Tangenten zu ermitteln. Dafür benötigen wir natürlich die erste Ableitung, die wir vorweg berechnen müssen. Um  zu bilden, multiplizieren wir in der Funktionsgleichung
zu bilden, multiplizieren wir in der Funktionsgleichung 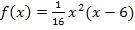 erst einmal das
erst einmal das 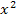 mit der Klammer, damit wir die Produktregel nicht anwenden müssen. Funktionen, die ein Produkt darstellen, das in beiden Faktoren x enthält, müssen schließlich mit der Produktregel abgeleitet werden. (Vergleiche auch:Weitere Ableitungsregeln) Den Aufwand beim Ableiten nach der Produktregel wollen wir uns ersparen. Da multiplizieren wir vor dem Ableiten doch lieber aus. Der Faktor
mit der Klammer, damit wir die Produktregel nicht anwenden müssen. Funktionen, die ein Produkt darstellen, das in beiden Faktoren x enthält, müssen schließlich mit der Produktregel abgeleitet werden. (Vergleiche auch:Weitere Ableitungsregeln) Den Aufwand beim Ableiten nach der Produktregel wollen wir uns ersparen. Da multiplizieren wir vor dem Ableiten doch lieber aus. Der Faktor 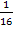 muss nicht in die Klammer hineinmultipliziert werden. Es handelt sich dabei um eine multiplikative Konstante, also um eine Zahl ohne x, mit der multipliziert wird, und solche Konstanten bleiben beim Ableiten einfach stehen. (Es kommt aber auch das richtige Ergebnis heraus, wenn du den Faktor
muss nicht in die Klammer hineinmultipliziert werden. Es handelt sich dabei um eine multiplikative Konstante, also um eine Zahl ohne x, mit der multipliziert wird, und solche Konstanten bleiben beim Ableiten einfach stehen. (Es kommt aber auch das richtige Ergebnis heraus, wenn du den Faktor 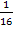 mit dem
mit dem 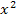 zusammen in die Klammer hineinmultiplizierst und dann ableitest. Das ist nur etwas unangenehmer zu rechnen wegen der entstehenden Brüche. Deshalb besser den Bruch nicht in die Klammer hineinmultiplizieren!)
zusammen in die Klammer hineinmultiplizierst und dann ableitest. Das ist nur etwas unangenehmer zu rechnen wegen der entstehenden Brüche. Deshalb besser den Bruch nicht in die Klammer hineinmultiplizieren!)
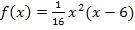
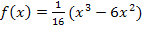
In dieser Form lässt sich die Ableitung leicht bilden.
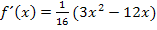
Wir klammern gleich noch 3x aus. Dadurch entsteht ein Produkt und das lässt sich leichter gleich Null setzen.
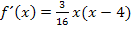
Nun setzen wir die Ableitung gleich Null. Die Lösungen lassen sich sofort erkennen.
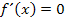
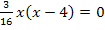
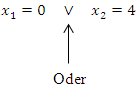
Dir ist nicht klar, wie man auf die beiden Lösungen kommt? Dann bedenke, dass ein Produkt gleich Null ist, wenn einer der Faktoren Null ist. Deshalb dürfen wir die Faktoren 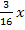 und
und 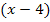 einzeln gleich Null setzen.
einzeln gleich Null setzen.
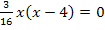
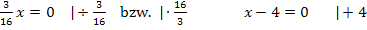

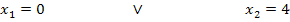
Jetzt kennen wir die x-Koordinaten der Punkte mit waagrechten Tangenten.

