Zweite Ableitung f´´(x)
Wenn dir nicht klar ist, warum der Graph  im Wendepunkt entweder am flachsten oder am steilsten verläuft, denkst du dir noch einige zusätzliche Tangenten an den Funktionsgraph dazu gezeichnet und überlegst dir, welche Steigung sie jeweils haben. Verlaufen die Tangenten zum Wendepunkt hin immer steiler oder immer flacher?
im Wendepunkt entweder am flachsten oder am steilsten verläuft, denkst du dir noch einige zusätzliche Tangenten an den Funktionsgraph dazu gezeichnet und überlegst dir, welche Steigung sie jeweils haben. Verlaufen die Tangenten zum Wendepunkt hin immer steiler oder immer flacher?
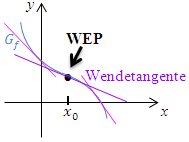
Abb.: Graph
Die Wendetangente (lila) fällt weniger als alle anderen Tangenten (rosa) in der Umgebung des Wendepunktes |
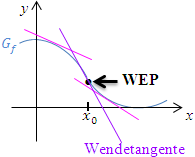
Abb.: Graph
Die Wendetangente (lila) fällt stärker als alle anderen Tangenten (rosa) in der Umgebung des Wendepunktes |
Einen Sonderfall stellen Wendepunkte mit waagrechter Tangente dar;sie heißen Terrassenpunkte. Terrassenpunkte sind also Wendepunkte mit waagrechter Tangente.
![]()
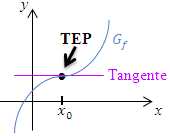
Abb.: Monoton steigender Graph und waagrechter Tangente
Links vom TEP ist der Graph rechtsgekrümmt, rechts davon ist er linksgekrümmt. Im TEP ändert sich somit das Krümmungsverhalten. |
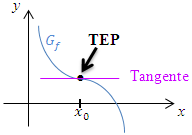
Abb.: Monoton fallender Graph und waagrechter Tangente
Links vom TEP ist der Graph linksgekrümmt, rechts davon verläuft er rechtsgekrümmt. Im TEP ändert sich somit das Krümmungsverhalten. |
Zusammenhang der Graphen 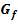 der Funktion selbst und
der Funktion selbst und 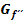 ihrer zweiten Ableitung
ihrer zweiten Ableitung
Ebenso wie  und die (erste) Ableitungsfunktion
und die (erste) Ableitungsfunktion  stellt auch die zweite Ableitung
stellt auch die zweite Ableitung  selbst eine Funktion dar. Jedem x wird durch
selbst eine Funktion dar. Jedem x wird durch  die Krümmung von
die Krümmung von  an der entsprechenden Stelle x zugeordnet.
an der entsprechenden Stelle x zugeordnet.
Wo der Graph von  linksgekrümmt ist, ist
linksgekrümmt ist, ist 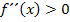 und der Graph von
und der Graph von  verläuft oberhalb der x-Achse. Entsprechend verläuft der Graph von
verläuft oberhalb der x-Achse. Entsprechend verläuft der Graph von  unterhalb der x-Achse, wo der Graph von
unterhalb der x-Achse, wo der Graph von  rechtsgekrümmt ist. An der Stelle, wo der Graph
rechtsgekrümmt ist. An der Stelle, wo der Graph  einen Wendepunkt hat, ist eine Nullstelle mit Vorzeichenwechsel des Graphen
einen Wendepunkt hat, ist eine Nullstelle mit Vorzeichenwechsel des Graphen  und
und  schneidet dort die x-Achse.
schneidet dort die x-Achse.
Verlauf des Graphen  der Funktion der Funktion  |
Verlauf des Graphen  der zweiten Ableitung der zweiten Ableitung  |
| linksgekrümmt | oberhalb der x-Achse |
| rechtsgekrümmt | unterhalb der x-Achse |
| Wendepunkt
(„Umlenkstelle“) |
Nullstelle mit Vorzeichenwechsel
(die x-Achse wird geschnitten und nicht bloßberührt) |
Vom Verlauf des Graphen  kann eindeutig auf den Graph
kann eindeutig auf den Graph  geschlossen werden, aber nicht umgekehrt.
geschlossen werden, aber nicht umgekehrt.

