Zweite Ableitung f´´(x)
Daher ist 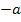 auf jeden Fall kleiner als a und steht in der Krümmungstabelle links von a. (Wäre
auf jeden Fall kleiner als a und steht in der Krümmungstabelle links von a. (Wäre 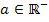 gewesen, wäre es nämlich genau umgekehrt. Für
gewesen, wäre es nämlich genau umgekehrt. Für 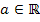 hätte man eine Fallunterscheidung machen müssen. Das bleibt uns hier jedoch erspart.)
hätte man eine Fallunterscheidung machen müssen. Das bleibt uns hier jedoch erspart.)
Krümmungstabelle:
| x | 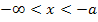 |
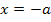 |
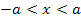 |
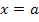 |
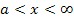 |
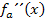 |
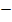 |
0 | 0 | 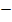 |
|
 |
rechtsgekrümmt | WEP | linksgekrümmt | WEP | rechtsgekrümmt |
Nebenrechnung zur Vorzeichenermittlung:
Hier noch einmal die zweite Ableitung: 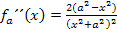
Als Beispiel für den Bereich 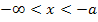 haben wir
haben wir 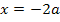 gewählt.
gewählt.
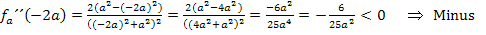
Als Beispiel für den Bereich 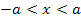 haben wir
haben wir 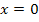 gewählt.
gewählt.
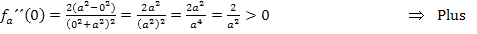
Als Beispiel für den Bereich 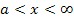 haben wir
haben wir 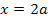 gewählt.
gewählt.
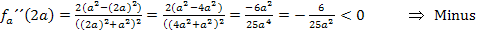
Da sich jeweils an den Stellen 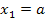 und
und 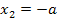 das Vorzeichen der zweiten Ableitung ändert, handelt sich bei beiden um Wendestellen. Wir berechnen als nächstes die beiden y-Koordinaten. Dazu setzten wir
das Vorzeichen der zweiten Ableitung ändert, handelt sich bei beiden um Wendestellen. Wir berechnen als nächstes die beiden y-Koordinaten. Dazu setzten wir 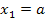 und
und 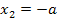 jeweils in die Funktionsgleichung
jeweils in die Funktionsgleichung 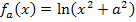 ein.
ein.
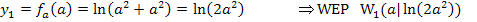
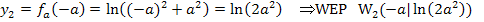
Schritt 3:Steigung der Wendetangenten in Abhängigkeit von a berechnen
Um die Steigung der Wendetangenten zu ermitteln, setzen wir die x-Koordinaten der Wendepunkte in die erste Ableitung ein.
Hier noch einmal die erste Ableitung: 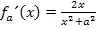
Steigung im 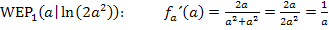
Steigung im 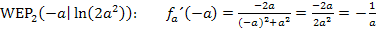
Schritt 4:Steigung der Wendetangenten gleich 2 setzen
Da die Wendetangente parallel zu der Gerade 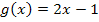 verlaufen soll, muss die Wendetangente die gleiche Steigung wie die Gerade
verlaufen soll, muss die Wendetangente die gleiche Steigung wie die Gerade 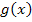 , also die Steigung 2, haben. Deshalb setzen wir die Steigung der Wendetangenten, die wir soeben in Abhängigkeit von a berechnet haben, jeweils gleich 2 und lösen dann nach a auf.
, also die Steigung 2, haben. Deshalb setzen wir die Steigung der Wendetangenten, die wir soeben in Abhängigkeit von a berechnet haben, jeweils gleich 2 und lösen dann nach a auf.




Der zweite für a berechnete Wert ist negativ;er kommt als Lösung nicht in Frage, da laut Angabe 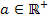 gelten muss. Der gesuchte Wert ist somit
gelten muss. Der gesuchte Wert ist somit 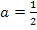 . Fertig!
. Fertig!
Fassen wir noch einmal das Wichtigste rund um die zweite Ableitung kurz zusammen.
Die zweite Ableitung 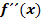 entspricht der Krümmung der Funktion entspricht der Krümmung der Funktion 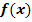 . .
|
| Wendepunkt (WEP) berechnen:
· Zweite Ableitung · Zweite Ableitung gleich Null setzen und nach x auflösen:
· y-Koordinate d.h. x-Koordinate · Nachweis des WEP: 1. Möglichkeit:Vorzeichenwechsel von 2. Möglichkeit:Mit der dritten Ableitung x-Koordinate
|

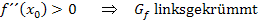
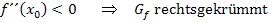
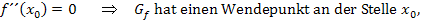
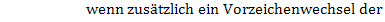
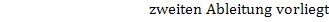
 bilden
bilden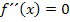
 x-Koordinate
x-Koordinate 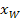 des WEP
des WEP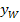 des WEP berechnen:
des WEP berechnen: 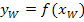
 einsetzen
einsetzen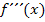 einsetzen
einsetzen
