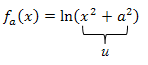Zweite Ableitung f´´(x)
Die äußere Funktion ist die ln-Funktion, die innere ist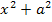 
. Wir bezeichnen die innere Funktion mit u. Bekanntlich ergibt 
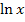nach x abgeleitet 
und entsprechend 
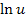nach u abgeleitet 
. Da u hier aber für die von x abhängige, innere Funktion 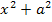steht, muss noch mit der Ableitung der inneren Funktion nachdifferenziert werden. Das heißt, es muss noch mit 
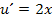multipliziert werden. 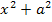ergibt abgeleitet schließlich 
. 
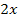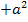fällt beim Ableiten nach x weg, weil es sich praktisch um eine konkrete Zahl handelt, die addiert wird. (Wenn dir nicht einleuchtet, warum hier 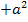beim Ableiten wegfällt, denke dir doch einfach irgendeine bestimmte Zahl für a, zum Beispiel 3. Wie würdest du denn 
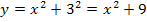ableiten? Dabei ist doch auch die Ableitung 
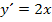. Die Zahl +9 fällt beim Ableiten weg. Entsprechend fällt auch 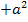beim Ableiten nach x weg.)
Laut Kettenregel:
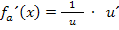
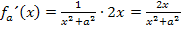
Wenn du nicht verstehst, wie die Kettenregel funktioniert, arbeite bitte unbedingt noch einmal den Teil Weitere Ableitungsregelndurch! Dort wird die Kettenregel ausführlich erklärt.
Nun bilden wir die zweite Ableitung. Wir verwenden die Quotientenregel.
Zur Erinnerung:
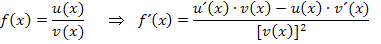
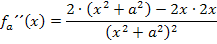
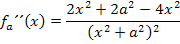
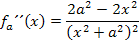
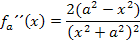
Schritt 2:Wendepunkt in Abhängigkeit von a berechnen
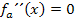
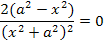
Ein Bruch ist gleich Null, wenn der Zähler Null ist (und der Nenner nicht gleich Null ist). Das bedeutet, dass wir einfach den Zähler gleich Null setzen und nach x auflösen dürfen. (Der Nenner kann hier gar nicht Null ergeben;er ist immer positiv. Wir können ihn komplett ignorieren.) Nicht klar? Ausführlichere Erklärung zum Weglassen des Nenners im 5. Bsp.
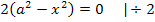
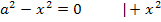
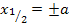
Vorsicht! Plus/Minus nicht vergessen! Neben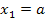 
gibt es auch die Lösung 
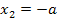, wegen: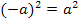 
Wir wissen nun, dass an den Stellen 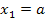und 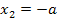die zweite Ableitung gleich Null ist. Vermutlich handelt es sich um Wendestellen, doch das müssen wir erst noch nachweisen. Wir untersuchen daher das Krümmungsverhalten. Nur wenn ein Vorzeichenwechsel der zweiten Ableitung vorliegt, handelt es sich tatsächlich um Wendestellen. Das gilt es nun nachzuweisen.
Hier noch einmal die zweite Ableitung: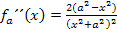 
Der Nenner ist offensichtlich immer positiv, egal was man für x einsetzt. Das Vorzeichen des Bruchs ist somit nur vom Zähler abhängig. Es würde also ausreichen nur das Vorzeichen des Zählers zu ermitteln. In der unten gezeigten Nebenrechnung zur Vorzeichenermittlung von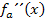 
wird aber dennoch die komplette zweite Ableitung verwendet. Da laut Angabe gilt 
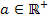, stellt a immer eine positive Zahl dar und 
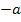immer eine negative Zahl.
