Zweite Ableitung f´´(x)
Der Schnittpunkt mit der x-Achse ist schließlich die Nullstelle und Nullstellen berechnet man bekanntlich, indem man die Funktion gleich Null setzt und nach x auflöst.
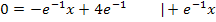
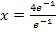
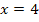
Im Punkt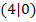 
wird die x-Achse von der Wendetangente geschnitten. Fertig!
5. Bsp.:Aus dem Schulheft einer Abiturientin
Wir betrachten die Funktionenschar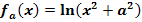 
mit 
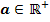. Wie muss der Scharparameter a gewählt werden, damit die Wendetangente parallel zur Geraden 
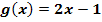verläuft?
Lösung:
Es liegt hier eine Funktionenschar vor, d.h. je nachdem welche Zahl für den Scharparameter a eingesetzt wird, ergibt sich eine andere Funktion. Bevor man eine der zur Schar gehörigen Funktionen zeichnen kann, muss also der Scharparameter a festgelegt sein. Der Scharparameter stellt somit eine feste Zahl dar und ist keine Variable, wie etwa x. Wir wissen zwar noch nicht, was a ist, dennoch ist a wie eine konkrete Zahl zu behandeln. Beim Ableiten musst du dich ausschließlich auf die Potenzen von x konzentrieren, wir leiten schließlich nach x ab und nicht nach a.
Wenn dir bei dieser Aufgabe noch nicht ganz klar ist, wie du vorgehen sollst, überlege dir vorweg, wann zwei Geraden zueinander parallel verlaufen. Dir ist sicher klar, dass zwei Geraden nur dann parallel sind, wenn sie die Gleiche Steigung besitzen. Die Frage ist hier, für welchen Wert von a die Wendetangente parallel zur Geraden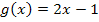 
ist. Da die Gerade 
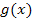die Steigung 2 besitzt, muss dann auch die Wendetangente die Steigung 2 haben. Wir müssen also letztendlich a so bestimmen, dass die Wendetangente die Steigung 2 hat. Aber wie geht das? Zuerst müssen wir den Wendepunkt in Abhängigkeit von a berechnen. (In Abhängigkeit von a bedeutet, dass wir mit a rechnen als wäre es eine Zahl. Wir dürfen dabei aber nichts für a einsetzen.) Nachdem wir den Wendepunkt in Abhängigkeit von a ermittelt haben, berechnen wir die Steigung der Wendetangente wieder in Abhängigkeit von a und setzen das Ergebnis gleich 2. Dadurch erhalten wir eine Gleichung mit der Unbekannten a, die wir nur noch nach a auflösen müssen. Wenn dir das soweit klar ist, kannst du jetzt gleich selbst versuchen die Aufgabe zu lösen. Wenn dir das alles noch nicht so wirklich einleuchtet, schaust du dir einfach die folgende Lösung genau an und versuchst sie Schritt für Schritt nachzuvollziehen.
Hier noch einmal die Funktionsgleichung: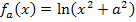 
mit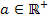 
Schritt 1:Erste und zweite Ableitung bilden
Um die erste Ableitung zu berechnen, brauchen wir die Kettenregel, da es sich bei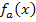 
um eine verkettete Funktion handelt.
