Zweite Ableitung f´´(x)
Man braucht hier nämlich auch noch die Kettenregel! (Probleme beim Ableiten dieser Funktion? Dann wiederhole am besten den Teil:Weitere Ableitungsregeln)
Schritt 1: Erste und zweite Ableitung bilden
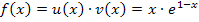
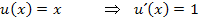
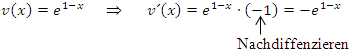
Laut Produktregel gilt:
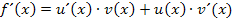
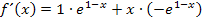
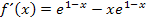
Wir klammern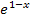 
aus. Das ergibt:
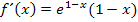
Nun berechnen wir die zweite Ableitung. Dafür muss wieder die Produktregel angewendet werden. Um den ersten Faktor abzuleiten, muss wieder nachdifferenziert werden, also noch einmal die Kettenregel angewendet werden.
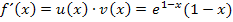
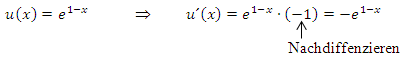
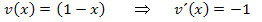
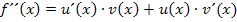
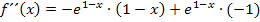
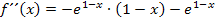
Wir klammern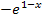 
aus. Das ergibt:
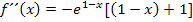
Die runden Klammern sind eigentlich nicht nötig. sie wurden nur gesetzt, damit du leichter nachvollziehen kannst, wie ausgeklammert wurde. Wir lassen die runden Klammern nun weg.
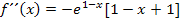
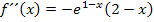
Schritt 2:Wendepunkt berechnen
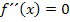
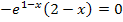
Ein Produkt ist gleich Null, wenn einer der Faktoren Null ist. Der Ausdruck 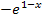kann nicht Null ergeben, er ist immer negativ, da 
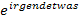immer positiv ist. Somit kann der Ausdruck 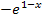einfach weggelassen werden und nur die Klammer gleich Null gesetzt werden. Dass die Klammer für 
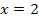Null ergibt ist offensichtlich. Daher folgt als einzige Lösung:
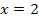
Dies ist die x-Koordinate des Wendepunktes. Wir müssen jedoch noch nachweisen, dass wirklich ein Wendepunkt vorliegt, also dass sich das Vorzeichen der zweiten Ableitung an der Stelle 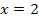ändert. Wir fertigen dazu eine Krümmungstabelle an.
Hier noch einmal die zweite Ableitung: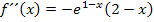
| x |  |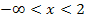
|
 |
 |
  |
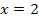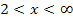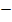0 |  |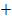
 |
rechtsgekrümmt | WEP | linksgekrümmt |
Nebenrechnung zur Vorzeichenermittlung von :
Als Beispielzahl für den Bereich 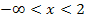haben wir 
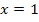gewählt.
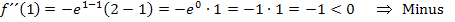
Als Beispielzahl für den Bereich 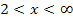haben wir 
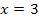gewählt.
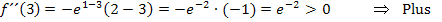
Damit haben wir den Vorzeichenwechsel der zweiten Ableitung nachgewiesen. Es handelt sich bei 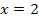sicher um eine Wendestelle. Nun berechnen wir noch die y-Koordinate des Wendepunkts. Dazu muss die x-Koordinate 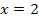in die Funktionsgleichung 
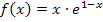eingesetzt werden.
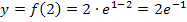
Der Wendepunkt hat somit die Koordinaten: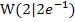 
Schritt 3:Wendetangente aufstellen
Hier noch einmal die erste Ableitung: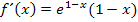
· Allgemeiner Ansatz: 
· Berechnung der Steigung:
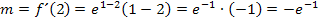
· Berechnung des y-Achsenabschnitts:
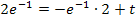
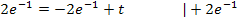
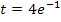
· Gleichung der Wendetangente:
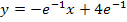
Schritt 4:Schnittpunkt der Wendetangente mit der x-Achse berechnen
Jeder Punkt der x-Achse hat die y-Koordinate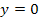 
. Daher setzen wir bei der Gleichung der Wendetangente für y Null ein, was dem Gleichnullsetzen der Gleichung entspricht.
