Zweite Ableitung f´´(x)
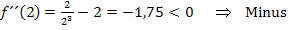
2. Möglichkeit:Wendepunkt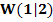 
mit der dritten Ableitung nachweisen
(Nur für Schüler, die das schon im Unterricht behandelt haben)
Von oben schon bekannt: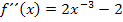 
Wir bilden die dritte Ableitung: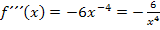 
x-Koordinate des (vermutlichen) Wendepunkts einsetzen: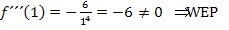 
Nun endlich zur Berechnung der Wendetangente, d.h. der Tangente im Punkt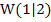 
. Eine Wendetangente ist bekanntlich die Tangente im Wendepunkt, also hier im Punkt 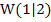. Sie wird genauso ermittelt wie jede andere Tangente in einem beliebigen Kurvenpunkt.
Zur Erinnerung:
Eine Tangente ist eine Gerade und hat somit eine Gleichung der Form 
. Die Steigung m erhält man, wenn man die x-Koordinate des Wendepunktes, hier 
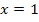, in die erste Ableitung einsetzt. (Die erste Ableitung entspricht ja der Steigung von 
.) Der y-Achsenabschnitt t wird berechnet, indem man die Koordinaten des Wendepunktes für x und y sowie die soeben berechnete Steigung für m in einsetzt und dann nach t auflöst.
Von oben schon bekannt: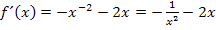 
Tangentengleichung im Punkt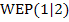 
aufstellen:
· Allgemeiner Ansatz:
· Berechnung der Steigung:
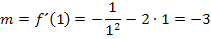
· Berechnung des y-Achsenabschnitts:
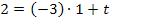
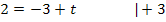
· Gleichung der Wendetangente:
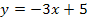
Das ist die Gleichung der gesuchten Wendetangente. Wir sind fertig!
Nun noch einige anspruchsvollere Beispiele rund um das Thema Wendepunkt und Wendetangente. Die folgenden zwei Beispiele setzen die Kenntnis der Funktionen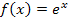 
und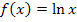 
voraus. Solltest du diese Funktionen im Unterricht noch nicht behandelt haben, überspringst du einfach die nächsten beiden Beispiele und gehst direkt zum Punkt „Art der Extrema untersuchen mit 
“.
4. Bsp.:
Wo schneidet die Wendetangente der Funktion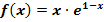 
die x-Achse?
Lösung:
Der Schnittpunkt mit der x-Achse wird bekanntlich auch als Nullstelle bezeichnet. Hier soll der Schnittpunkt der Wendetangente mit der x-Achse berechnet werden. Das heißt, es soll die Nullstelle der Wendetangente ermittelt werden. Dafür benötigen wir natürlich erst einmal die Gleichung der Wendetangente. Um sie aufstellen zu können, müssen wir vorweg die Koordinaten des Wendepunkts berechnen. Wie du weißt, gilt beim Wendepunkt: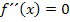 
Wir brauchen also die zweite Ableitung der Funktion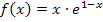 
. Deshalb müssen wir zweimal ableiten. Bilde doch gleich ´mal selbst die erste und zweite Ableitung! Bedenke, dass es sich bei dieser Funktion um ein Produkt handelt, das in beiden Faktoren x enthält, so dass die Produktregel angewendet werden muss. Beim Ableiten des zweiten Faktors Nachdifferenzieren nicht vergessen!
