Zweite Ableitung f´´(x)
Dafür muss man die erste Ableitung an den Stellen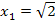 
und 
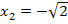berechnen. D.h. Man muss einmal 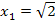und einmal 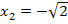in die erste Ableitung einsetzen und schauen, ob dabei Null herauskommt.
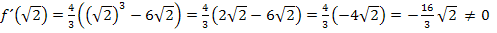
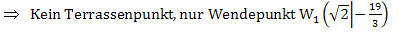
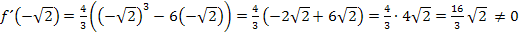
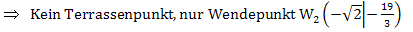
Wiederholung:Bedingungen für die Existenz eines Terrassenpunkts
Ein Terrassenpunkt (TEP) ist schließlich ein Wendepunkt mit waagrechter Tangente. Da die Tangente waagrecht verläuft, muss die Steigung an dieser Stelle, also die erste Ableitung, gleich Null sein. In diesem Beispiel handelt es sich bei keinem der beiden Wendepunkte um einen Terrassenpunkt, da sich für die erste Ableitung weder an der Stelle 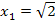noch an der Stelle 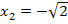Null ergibt.
Weil ein Terrassenpunkt auch ein Wendepunkt ist, muss dort die Krümmung, d.h. die zweite Ableitung, gleich Null sein. Damit sicher ein Wendepunkt vorliegt, darf jedoch die dritte Ableitung nicht gleich Null sein. (Alternativ zum Nachweis, dass die dritte Ableitung an der jeweiligen Stelle ungleich Null ist, kann auch der Vorzeichenwechsel der zweiten Ableitung verwendet werden.)
TEP: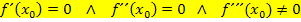 
Mehr dazu bei:Wendepunkte mit der dritten Ableitung nachweisen
3. Bsp.:
Berechne die Gleichung der Wendetangente der Funktion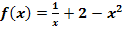 
.
Lösung:
Damit wir die Gleichung der Wendetangente ermitteln können, müssen wir vorweg die Koordinaten des Wendepunktes der Funktion berechnen. Ein Wendepunkt wird bekanntlich mit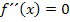 
ermittelt. Daher brauchen wir die zweite Ableitung. Wir leiten 
also zweimal ab. Dazu formen wir die Funktion mit dem Potenzgesetz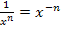 
um, damit wir mit der Ableitungsregel 
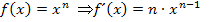arbeiten können. (Die Verwendung der Quotientenregel beim Ableiten von 
ist hier zu umständlich, wäre aber nicht falsch.)
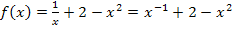
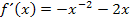
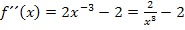
Nun berechnen wir den Wendepunkt:
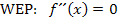
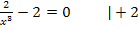
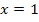
Die y-Koordinate des Wendepunktes W erhalten wir, wenn wir 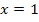in die Funktionsgleichung 
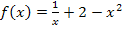einsetzen.
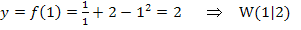
Dass es sich dabei wirklich um einen Wendepunkt handelt, muss noch speziell nachgewiesen werden.
Nachweis des Wendepunktes:
1. Möglichkeit:Wendepunkt mit Hilfe des Krümmungsverhaltens nachweisen
Damit es sich bei W(1|2) tatsächlich um einen Wendepunkt handelt, muss an der Stelle x = 1 ein Vorzeichenwechsel der zweiten Ableitung vorliegen. Wir müssen also zeigen, dass sich das Vorzeichen der zweiten Ableitung, also das Krümmungsverhalten, an der Stelle x = 1 ändert. Deshalb müssen wir das Krümmungsverhalten von 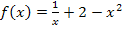untersuchen.
Untersuchung des Krümmungsverhaltens:
Beachte hier, dass die Funktion 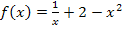bei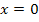 
eine Definitionslücke besitzt.
