Zweite Ableitung f´´(x)
Alternativ dazu kann in der Krümmungstabelle auch die Intervallschreibweise verwendet werden.
| x |  |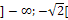
 |
 |
 |
 |
 |
 + |
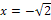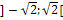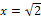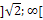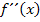0 |  |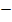
0 | + |
 |
links-gekrümmt | WEP | rechts-gekrümmt | WEP | links-gekrümmt |
Da sowohl bei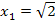 
als auch bei 
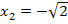ein Vorzeichenwechsel von 
vorliegt, handelt es sich tatsächlich an beiden Stellen um Wendestellen. Es ist somit nachgewiesen, dass die Funktion die Wendepunkte 
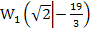und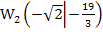 
besitzt.
Damit ist die Aufgabe gelöst.
Für Schüler eines Gymnasiums, aber nicht für FOS- Schüler:
Wenn dein(e) Lehrer(in) in der Schule keine Tabelle verwendet, um das Krümmungsverhalten zu untersuchen, schreibst du statt der Tabelle:
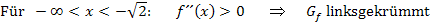
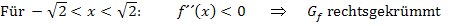
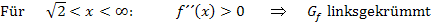
Dies ist nur eine andere Darstellungsart des Krümmungsverhaltens. Was in der Tabelle untereinander in den jeweiligen Spalten steht, wird dabei einfach nebeneinander geschrieben. Statt Plus schreibt man natürlich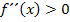 
und anstatt Minus entsprechend 
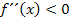. Die beiden Bereiche, wo der Graph linksgekrümmt ist, können auch zusammengefasst geschrieben werden. Das sieht dann folgendermaßen aus:
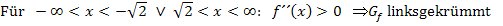
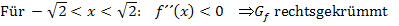
Alternativ dazu kannst du auch die Intervallschreibweise bei der Angabe der Krümmungsintervalle verwenden:
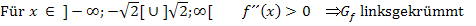
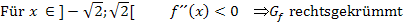
Ein extrem wichtiger Hinweis für alle Schüler einer FOS (in Bayern):Die Krümmungsintervalle müssen auf der FOS (in Bayern) mit eingeschlossenen Grenzen geschrieben werden! Genaueres dazu:Hinweis zu den Krümmungsintervallen
Für alle Schüler, die im Unterricht auch die dritte Ableitung behandelt haben:
Wie oben schon kurz erwähnt, kann der Nachweis, dass an der Stelle 
ein Wendepunkt vorliegt, auch mit Hilfe der dritten Ableitung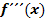 
geführt werden:
WEP: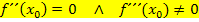 
Das bedeutet, dass man die x-Koordinate, die man erhalten hat, indem man gleich Null gesetzt hat, noch in die dritte Ableitung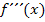 
einsetzen muss. Dann überprüft man, ob eine Zahl ungleich Null herauskommt. Wenn die dritte Ableitung an der Stelle 
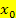nicht gleich Null ist, liegt dort sicher ein Wendepunkt vor.
Auf unser Beispiel bezogen:
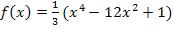
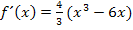
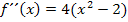
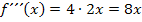
Oben haben wir die zweite Ableitung schon gleich Null gesetzt und nach x aufgelöst. Daher wissen wir:
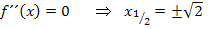
Um nachzuweisen, dass es sich wirklich um Wendepunkte handelt, müssen wir nun 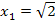und 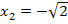jeweils in die dritte Ableitung einsetzen und zeigen, dass sich dabei nicht Null ergibt.
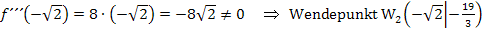
Ab hier wieder für alle Schüler:
Es soll zusätzlich noch überprüft werden, ob es sich eventuell bei einem oder beiden der Wendepunkte um einen Terrassenpunkt, also um einen Wendepunkt mit waagrechter Tangente, handelt.
