Zweite Ableitung f´´(x)

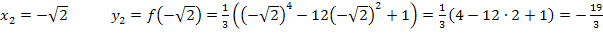
Anmerkung:Da die Funktion 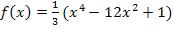nur gerade Potenzen von x enthält, ist sie achsensymmetrisch zur y-Achse. Es gilt: 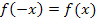und somit auch 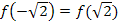. Deshalb hätte man sich die  Berechnung der zweiten y-Koordinate sparen können;es ist wegen der Achsensymmetrie zur y-Achse sowieso klar, dass sich für 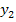das gleiche Ergebnis wie bei 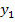ergibt.

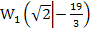Vermutlich hat die Funktion somit die beiden Wendepunkte und 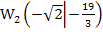. Dies muss aber noch nachgewiesen werden. Nur wenn sich bei 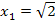und bei 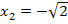jeweils das Vorzeichen der zweiten Ableitung ändert, liegen wirklich Wendepunkte vor. Wir müssen daher das Krümmungsverhalten untersuchen.

Nachweis der Wendepunkte:Untersuchung des Krümmungsverhaltens

Hier noch einmal die zweite Ableitung: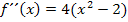

Wir zeichnen eine Tabelle der folgenden Form:

x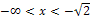
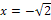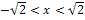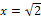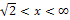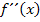		0		0

In die freien Spalten der mittleren Zeile werden wir die entsprechenden Vorzeichen der zweiten Ableitung eintragen. Um diese Vorzeichen zu ermitteln, denkst du dir am besten jeweils eine konkrete Zahl aus dem entsprechenden Bereich, setzt diese Zahlen nacheinander in 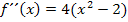ein und bestimmst die Vorzeichen des Ergebnisses.

So kannst du beispielsweise für den Bereich 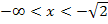die Zahl -2 wählen. ( 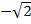ist näherungsweise 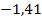. Das kannst du ja mit dem Taschenrechner ausrechnen.) Die Zahl -2 ist auf jeden Fall kleiner als 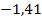. Setzt man -2 in die zweite Ableitung ein, ergibt sich 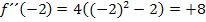, also ein positiver Wert. Daher schreiben wir ein Plus-Zeichen links in die mittlere Zeile.

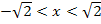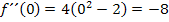Dann denken wir uns eine Zahl aus dem Bereich . Es bietet sich dabei die Zahl 0 an. Sie liegt sicher in diesem Intervall und es lässt sich bequem damit rechnen. Setzt man 0 in ein, erhält man , also einen negativen Wert. Wir schreiben daher in die Krümmungstabelle direkt unter 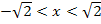ein Minuszeichen.

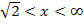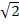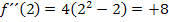Für den Bereich wählen wir beispielsweise die Zahl 2. Sie ist auf jeden Fall größer als , liegt also in diesem Intervall und es lässt sich leicht damit rechnen. Setzt man die Zahl 2 in ein, erhält man . Da sich ein positiver Wert ergibt, schreiben wir ein Plus in unsere Krümmungstabelle direkt unter .

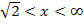Die Krümmungstabelle sieht nun folgendermaßen aus:

x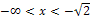
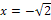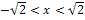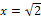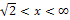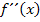	+	0		0	+

Jetzt müssen wir uns noch überlegen, was dies für das Krümmungsverhalten des Graphen bedeutet.

Zur Erinnerung:

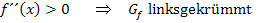
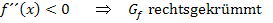
Die fertige Krümmungstabelle sieht dann so aus:

x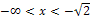
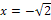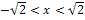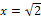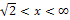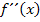	+	0		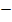0	+
	links-gekrümmt	WEP	rechts-gekrümmt	WEP	links-gekrümmt

---