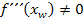Zweite Ableitung f´´(x)
Da sich das Vorzeichen der zweiten Ableitung an der Stelle  geändert hat, liegt natürlich ein Wendepunkt vor.
geändert hat, liegt natürlich ein Wendepunkt vor.
| Anleitung zur Berechnung von Wendepunkten:
Geg.: Berechnung der Wendepunkte · · D.h. zweite Ableitung gleich Null setzten und nach x auflösen. Das ergibt die x-Koordinate(n) · D.h. die x-Koordinate(n) des (vermutlichen) Wendepunktes bzw. der (vermutlichen) Wendepunkte jeweils in die Funktionsgleichung · Nachweis des Wendepunktes 1. Möglichkeit:Mit Untersuchung des Krümmungsverhaltens, z.B. mit Krümmungstabelle Wenn ein Vorzeichenwechsel von Die Krümmungstabelle wird im Prinzip angefertigt wie eine Monotonietabelle, aber an Stelle der ersten Ableitung wird natürlich das Vorzeichen der zweiten Ableitung bestimmt. (Wie das funktioniert, wird gleich in den Beispielaufgaben gezeigt.)
2. Möglichkeit:Mit dritter Ableitung (Nur für Schüler, die
D.h. die x-Koordinate(n) des Wendepunktes oder der Wendepunkte jeweils in die dritte Ableitung Diese Methode des Nachweises von Wendepunkten wird ausführlich im gesonderten Teil Wendepunkte mit der dritten Ableitung nachweisen besprochen.
|
Jetzt schauen wir uns doch endlich ein konkretes Beispiel an, wie man Wendepunkte berechnet und mit Hilfe des Krümmungsverhaltens der Funktion nachweist.
2. Bsp.:Gegeben ist die Funktion 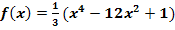 . Bestimme die Wendepunkte der Funktion! Handelt es sich dabei auch um Terrassenpunkte?
. Bestimme die Wendepunkte der Funktion! Handelt es sich dabei auch um Terrassenpunkte?
Lösung:
Zuerst bilden wir die erste und zweite Ableitung, da schließlich für Wendepunkte 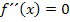 gilt und wir somit
gilt und wir somit  benötigen.
benötigen.
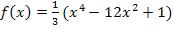
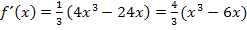 Beim letzten Schritt wurde die Zahl 4 ausgeklammert.
Beim letzten Schritt wurde die Zahl 4 ausgeklammert.
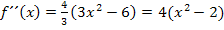 Beim letzten Schritt wurde die Zahl 3 ausgeklammert.
Beim letzten Schritt wurde die Zahl 3 ausgeklammert.
Nun setzen wir die zweite Ableitung gleich Null.
Wendepunkt: 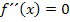
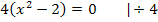
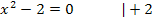

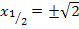 Vorsicht:Plus/Minus nicht vergessen!
Vorsicht:Plus/Minus nicht vergessen!
Nun wissen wir, dass nur bei 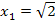 und bei
und bei 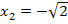 ein Wendepunkt sein kann.
ein Wendepunkt sein kann.
Um die y-Koordinaten zu berechnen, setzen wir die soeben ermittelten x-Koordinaten in die Funktionsgleichung 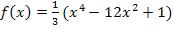 ein.
ein.  ist schließlich nur eine andere Schreibweise für y.
ist schließlich nur eine andere Schreibweise für y.
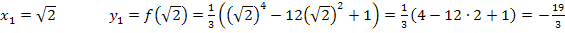

 und
und  aller Punkte, die für einen Wendepunkt in Frage kommen.
aller Punkte, die für einen Wendepunkt in Frage kommen.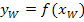
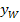 dieses Punktes bzw. Punkte.
dieses Punktes bzw. Punkte.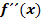 an der Stelle
an der Stelle 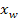 vorliegt, handelt es sich um einen Wendepunkt.
vorliegt, handelt es sich um einen Wendepunkt.
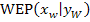
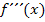 im Unterricht behandelt haben)
im Unterricht behandelt haben)