Nähere Erläuterungen zur Berechnung der Ableitung im Bsp. 3
Dir ist nicht klar, wie man die erste Ableitung der Funktionenschar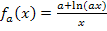 
bildet? Ok, dann mal ganz langsam. Wie schon oben erwähnt, brauchen wir die Quotientenregel:
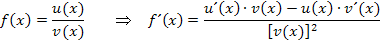
In unserem konkreten Fall gilt:
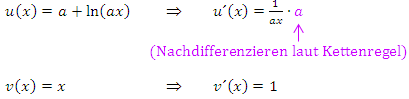
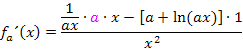
Die weitere Vereinfachung ist in der Lösung von Bsp. 3 bereits gezeigt. Falls du noch immer nicht verstanden hast, wie man auf diese Ableitung kommt, solltest du den Teil Weitere Ableitungsregelngenau durcharbeiten, vor allem Die Kettenregel. Um hier die Ableitung des Zählers zu bilden wird innerhalb der Quotientenregel die Kettenregel benötigt. Sie besagt, dass verkettete Funktionen abgeleitet werden, indem man zuerst nur die äußere Funktion ableitet und die innere dabei stehen lässt. Dann muss noch nachdifferenziert, also mit der Ableitung der inneren Funktion multipliziert werden.
Bei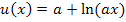 
fällt beim Ableiten das vordere a einfach weg, denn es handelt sich um eine additive Konstante (d.h. um eine Zahl ohne x, die addiert wird). Additive Konstanten fallen beim Ableiten immer weg, da sie abgeleitet 0 ergeben.
Die Funktion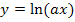 
ist eine verkettete Funktion, wobei 
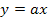die innere Funktion darstellt. Der ln ist somit die äußere Funktion. 
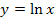ergibt abgeleitet bekanntlich 
.
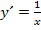Leitet man 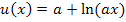nach x ab, ergibt sich entsprechend: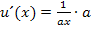 
Warum noch mit a multipliziert wird? Ganz einfach, weil das a die Ableitung der inneren Funktion 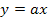ist und man laut Kettenregel noch nachdifferenzieren muss, also mit der Ableitung der inneren Funktion multiplizieren muss.
