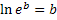Wendepunkte mit der dritten Ableitung nachweisen

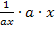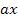Dazu kürzen wir den Ausdruck mit ;es bleibt die Zahl 1.

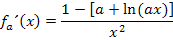
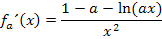
Berechnung der zweiten Ableitung:

Wir müssen 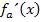noch einmal ableiten. Es wird dabei wiederum die Quotientenregel angewendet. Um den Zähler von 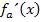abzuleiten, braucht man allerdings zusätzlich die Kettenregel. Die Kettenregel funktioniert nach dem gleichen Prinzip wie schon bei der Berechnung der Zählerableitung von 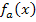. (Vergleiche oben!)

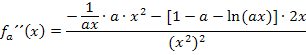
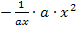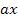Jetzt vereinfachen wir soweit möglich. Wir kürzen den Ausdruck mit ;es bleibt 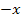. Außerdem multiplizieren wir die hintere Klammer des Zählers aus. Vorsicht:Das Minus vor der eckigen Klammer bezieht sich auf alles Folgende! Beim Auflösen der Klammer drehen sich daher alle Vorzeichen des Ausdrucks in der Klammer um. Im Nenner wenden wir das Potenzgesetzt 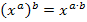an. Daher gilt: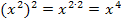

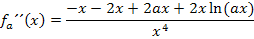
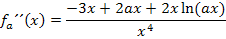
Nun klammern wir im Zähler x aus, damit man im nächsten Schritt mit x kürzen kann.

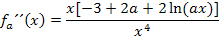
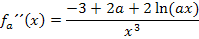
Berechnung der dritten Ableitung:

Wir müssen 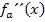noch einmal ableiten. Es wird dabei wiederum die Quotientenregel angewendet. Um den Zähler von 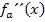abzuleiten, brauchen wir wieder zusätzlich die Kettenregel. Das ist das gleiche Prinzip wie schon bei der Berechnung zweiten Ableitung.

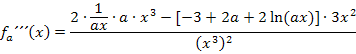
Die weitere Vereinfachung von 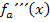geht ähnlich wie schon die oben gezeigte Vereinfachung von 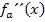. Im Zähler vorne kürzen mit ax, den hinteren Teil ausmultiplizieren und im Nenner das Potenzgesetz anwenden. So ergibt sich:

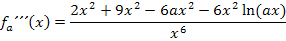
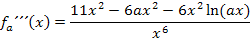
Nun klammern wir im Zähler 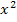aus, damit man im nächsten Schritt mit 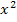kürzen kann.

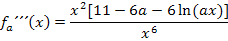
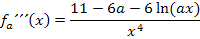
Hier noch einmal 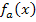mit allen ermittelten Ableitungen auf einen Blick:

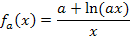
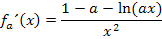
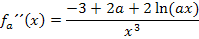
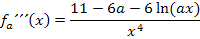
Berechnung des Extremums:

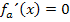
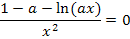
Ein Bruch ist gleich Null, wenn der Zähler gleich Null ist und der Nenner nicht gleich Null ist. Der Nenner kann sowieso nicht gleich Null werden, da 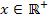gilt. Wir können also einfach den Zähler gleich Null setzten.

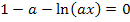
Auf diese Gleichung wärst du natürlich auch gekommen, wenn du einfach auf beiden Seiten der Gleichung mit dem Nenner 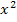multipliziert hättest, also das 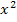auf die andere Seite der Gleichung gebracht hättest. Es gilt schließlich:

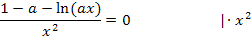
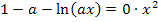
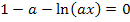
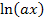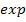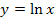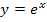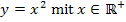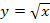Diese Gleichung lösen wir nun nach x auf, indem wir zuerst den Ausdruck isolieren und dann den ln mit , d.h. „e hoch …“ , beseitigen. Die Funktionen und sind zueinander Umkehrfunktionen, d.h. sie heben sich gegenseitig auf, so wie sich zum Beispiel auch Wurzel und Quadrat gegenseitig aufheben. Auch und sind zueinander Umkehrfunktionen. Siehe auch:Umkehrfunktion 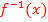Daher gilt: 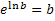und

---