Wendepunkte mit der dritten Ableitung nachweisen
Oder mit rationalem Nenner bei der x-Koordinate:
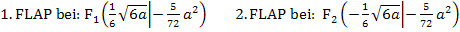
Nun zur nächsten Frage. Für welche Werte von a handelt es sich bei den Flachpunkten sogar um Wendepunkte? Wendepunkte sind nur diejenigen Flachpunkte, wo auch ein Vorzeichenwechsel von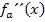 
vorliegt bzw. wo die dritte Ableitung ungleich Null ist. Wir nehmen daher die dritte Ableitung 
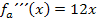, setzten die x-Koordinaten der Flachpunkte ein und überlegen uns dann, für welche Werte von a das Ergebnis ungleich Null ist.
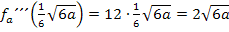
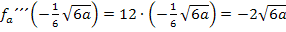
Für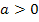 
liegen tatsächlich Wendepunkte vor, weil dann die dritte Ableitung nicht Null ist. Für 
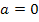gibt es nur einen Flachpunkt an der Stelle 
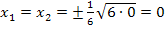, die beiden x-Koordinaten fallen praktisch zusammen. Für 
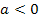existieren überhaupt keine Flachpunkte. Das erkennt man daran, dass a unter der Wurzel steht. Würde man für a einen negativen Wert wählen, wäre die Wurzel bei 
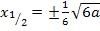gar nicht definiert. Das haben wir oben schon besprochen.
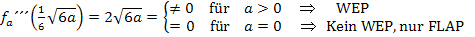
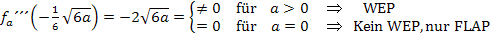
Nun müssen wir a noch so bestimmen, dass genau an der Stelle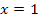 
ein Wendepunkt ist. Wir haben die x-Koordinaten der Wendepunkte vorher schon in Abhängigkeit von a ermittelt:Daher wissen wir bereits, dass für 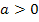an den Stellen 
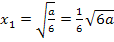und 
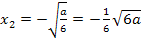Wendepunkte vorliegen. Entwe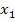der 
oder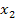 
muss jetzt 1 ergeben. Welche nimmt dann jetzt? Ganz einfach! Nur die 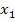– Koordinate! Die 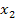– Koordinate ist nämlich immer negativ, weil vor der Wurzel ein Minus steht. 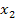kann somit nicht gleich 1 sein;es kommt nur noch die andere x-Koordinate 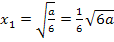in Frage. Diese x – Koordinate müssen wir nun gleich 1 setzten und dann nach a auflösen. Mit 
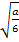rechnet es sich etwas leichter als mit 
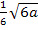. Deshalb arbeiten wir lieber mit der Form .
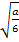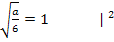
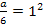
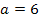
Somit wissen wir, dass nur für 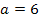bei 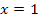ein Wendepunkt vorliegt. Wir brauchen nur noch den ermittelten Wert für a in die Funktionsgleichung 
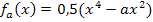einsetzen.
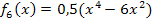
Dies ist die Gleichung derjenigen Scharfunktion, welche bei 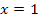ein Wendepunkt besitzt. Damit ist die Aufgabe vollständig gelöst.
Damit du dir die Schar 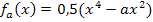besser vorstellen kannst, hier die Graphen einiger ausgewählter Funktionen der Schar.
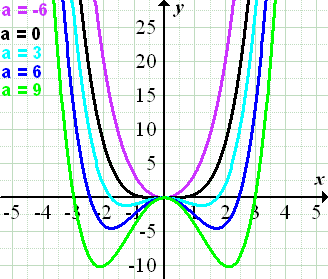
Abb.: Die Graphen der Schar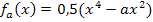
Ergänzende Erläuterungen zur Abbildung:
An der Abbildung ist zu erkennen, dass nur die Graphen zu positiven Parameterwerten a Wendepunkte besitzen, d.h. der hellblaue, der dunkelblaue und der grüne Graph. Der Graph zu a = 0, d.h. der schwarze Graph, hat an der Stelle x = 0 einen Flachpunkt, aber keinen Wendepunkt. (Man lenkt bei dem schwarzen Graph an der Stelle x = 0 nicht um.
